原创

Graduate Texts in Mathematics

List of books[edit]

1. Introduction to Axiomatic Set Theory, Gaisi Takeuti, Wilson M. Zaring (1982, 2nd ed., ISBN 978-1-4613-8170-9)
2. Measure and Category – A Survey of the Analogies between Topological and Measure Spaces, John C. Oxtoby (1980, 2nd ed., ISBN 978-0-387-90508-2)
3. Topological Vector Spaces, H. H. Schaefer, M. P. Wolff (1999, 2nd ed., ISBN 978-0-387-98726-2)
4. A Course in Homological Algebra, Peter Hilton, Urs Stammbach (1997, 2nd ed., ISBN 978-0-387-94823-2)
5. Categories for the Working Mathematician, Saunders Mac Lane (1998, 2nd ed., ISBN 978-0-387-98403-2)
6. Projective Planes, Daniel R. Hughes, Fred C. Piper, (1982, ISBN 978-3-540-90043-6)
7. A Course in Arithmetic, Jean-Pierre Serre (1996, ISBN 978-0-387-90040-7)
8. Axiomatic Set Theory, Gaisi Takeuti, Wilson M. Zaring, (1973, ISBN 978-3-540-90050-4)
9. Introduction to Lie Algebras and Representation Theory, James E. Humphreys (1997, ISBN 978-0-387-90053-7)
10. A Course in Simple-Homotopy Theory, Marshall. M. Cohen, (1973, ISBN 0-387-90056-X)
11. Functions of One Complex Variable I, John B. Conway (1978, 2nd ed., ISBN 978-0-387-90328-6)
12. Advanced Mathematical Analysis, Richard Beals (1973, ISBN 978-0-387-90065-0)
13. Rings and Categories of Modules, Frank W. Anderson, Kent R. Fuller (1992, 2nd ed., ISBN 978-0-387-97845-1)
14. Stable Mappings and Their Singularities, Martin Golubitsky, Victor Guillemin, (1974, ISBN 978-0-387-90072-8)
15. Lectures in Functional Analysis and Operator Theory, Sterling K. Berberian, (1974, ISBN 978-0-387-90080-3)
16. The Structure of Fields, David J. Winter, (1974, ISBN 978-3-540-90074-0)
17. Random Processes, Murray Rosenblatt, (1974, ISBN 978-0-387-90085-8)
18. Measure Theory, Paul R. Halmos (1974, ISBN 978-0-387-90088-9)
19. A Hilbert Space Problem Book, Paul R. Halmos (1982, 2nd ed., ISBN 978-0-387-90685-0)
20. Fibre Bundles, Dale Husemoller (1994, 3rd ed., ISBN 978-0-387-94087-8)
21. Linear Algebraic Groups, James E. Humphreys (1975, ISBN 978-0-387-90108-4)
22. An Algebraic Introduction to Mathematical Logic, Donald W. Barnes, John M. Mack (1975, ISBN 978-0-387-90109-1)
23. Linear Algebra, Werner H. Greub (1975, ISBN 978-0-387-90110-7)
24. Geometric Functional Analysis and Its Applications, Richard B. Holmes, (1975, ISBN 978-0-387-90136-7)
25. Real and Abstract Analysis, Edwin Hewitt, Karl Stromberg (1975, ISBN 978-0-387-90138-1)
26. Algebraic Theories, Ernest G. Manes, (1976, ISBN 978-3-540-90140-2)
27. General Topology, John L. Kelley (1975, ISBN 978-0-387-90125-1)
28. Commutative Algebra I, Oscar Zariski, Pierre Samuel (1975, ISBN 978-0-387-90089-6)
29. Commutative Algebra II, Oscar Zariski, Pierre Samuel (1975, ISBN 978-0-387-90171-8)
30. Lectures in Abstract Algebra I: Basic Concepts, Nathan Jacobson (1976, ISBN 978-0-387-90181-7)
31. Lectures in Abstract Algebra II: Linear Algebra, Nathan Jacobson (1984, ISBN 978-0-387-90123-7)
32. Lectures in Abstract Algebra III: Theory of Fields and Galois Theory, Nathan Jacobson (1976, ISBN 978-0-387-90168-8)
33. Differential Topology, Morris W. Hirsch (1976, ISBN 978-0-387-90148-0)
34. Principles of Random Walk, Frank Spitzer (1964, 2nd ed., ISBN 978-1-4757-4229-9)
35. Several Complex Variables and Banach Algebras, Herbert Alexander, John Wermer (1998, 3rd ed., ISBN 978-0-387-98253-3)
36. Linear Topological Spaces, John L. Kelley, Isaac Namioka (1982, ISBN 978-0-387-90169-5)
37. Mathematical Logic, J. Donald Monk (1976, ISBN 978-0-387-90170-1)
38. Several Complex Variables, H. Grauert, K. Fritzsche (1976, ISBN 978-0-387-90172-5)
39. An Invitation to {\displaystyle C^{*}}-Algebras, William Arveson (1976, ISBN 978-0-387-90176-3)
40. Denumerable Markov Chains, John G. Kemeny, J. Laurie Snell, Anthony W. Knapp, D.S. Griffeath (1976, ISBN 978-0-387-90177-0)
41. Modular Functions and Dirichlet Series in Number Theory, Tom M. Apostol (1989, 2nd ed., ISBN 978-0-387-97127-8)
42. Linear Representations of Finite Groups, Jean-Pierre Serre, Leonhard L. Scott (1977, ISBN 978-0-387-90190-9)
43. Rings of Continuous Functions, Leonard Gillman, Meyer Jerison (1976, ISBN 978-0-387-90198-5)
44. Elementary Algebraic Geometry, Keith Kendig (1977, ISBN 978-0-387-90199-2)[1]
45. Probability Theory I, M. Loève (1977, 4th ed, ISBN 978-0-387-90210-4)
46. Probability Theory II, M. Loève (1978, 4th ed, ISBN 978-0-387-90262-3)
47. Geometric Topology in Dimensions 2 and 3, Edwin E. Moise (1977, ISBN 978-0-387-90220-3)
48. General Relativity for Mathematicians, R. K. Sachs, H. Wu (1983, ISBN 978-0-387-90218-0)
49. Linear Geometry, K. W. Gruenberg, A. J. Weir (1977, 2nd ed., ISBN 978-0-387-90227-2)
50. Fermat’s Last Theorem: A Genetic Introduction to Algebraic Number Theory, Harold M. Edwards (2000, ISBN 978-0-387-90230-2)
51. A Course in Differential Geometry, William Klingenberg, D. Hoffman (1983, ISBN 978-0-387-90255-5)
52. Algebraic Geometry, Robin Hartshorne (2010, ISBN 978-1-4419-2807-8)
53. A Course in Mathematical Logic for Mathematicians, Yu. I. Manin, Boris Zilber (2009, 2nd ed., ISBN 978-1-4419-0614-4)
54. Combinatorics with Emphasis on the Theory of Graphs, Mark E. Watkins, Jack E. Graver (1977, ISBN 978-0-387-90245-6)
55. Introduction to Operator Theory I: Elements of Functional Analysis, Arlen Brown, Carl Pearcy (1977, ISBN 978-0-387-90257-9)
56. Algebraic Topology: An Introduction, William S. Massey (1977, ISBN 978-0-387-90271-5)
57. Introduction to Knot Theory, Richard H. Crowell, Ralph H. Fox (1977, ISBN 978-0-387-90272-2)
58. p-adic Numbers, p-adic Analysis, and Zeta-Functions, Neal Koblitz (1984, 2nd ed., ISBN 978-0-387-96017-3)
59. Cyclotomic Fields, Serge Lang (1978, ISBN 978-0-387-90307-1)[2]
60. Mathematical Methods of Classical Mechanics, V. I. Arnold, A. Weinstein, K. Vogtmann (1989, 2nd ed., ISBN 978-0-387-96890-2)
61. Elements of Homotopy Theory, George W. Whitehead (1978, ISBN 978-0-387-90336-1)
62. Fundamentals of the Theory of Groups, M. I. Kargapolov, J. I. Merzljakov (1979, ISBN 978-1-4612-9966-0)
63. Graph Theory – An Introductory Course, Béla Bollobás (1979, ISBN 978-1-4612-9969-1)
64. Fourier Series – A Modern Introduction Volume 1, R. E. Edwards (1979, 2nd ed., ISBN 978-1-4612-6210-7)
65. Differential Analysis on Complex Manifolds, Raymond O. Wells, Jr. (2008, 3rd ed., ISBN 978-0-387-73891-8)
66. Introduction to Affine Group Schemes, W. C. Waterhouse (1979, ISBN 978-1-4612-6219-0)
67. Local Fields, Jean-Pierre Serre (1979, ISBN 978-0-387-90424-5)
68. Linear Operators in Hilbert Spaces, Joachim Weidmann [de] (1980, ISBN 978-1-4612-6029-5)
69. Cyclotomic Fields II, Serge Lang (1980, ISBN 978-1-4684-0088-5)
70. Singular Homology Theory, William S. Massey (1980, ISBN 978-1-4684-9233-0)
71. Riemann Surfaces, Herschel Farkas [de], Irwin Kra (1992, 2nd ed., ISBN 978-0-387-97703-4)
72. Classical Topology and Combinatorial Group Theory, John Stillwell (1980, 2ed 1993, ISBN 978-0-3879-7970-0)
73. Algebra, Thomas W. Hungerford (1974, ISBN 978-0-387-90518-1)
74. Multiplicative Number Theory, Harold Davenport, Hugh Montgomery (2000, 3rd ed., ISBN 978-0-387-95097-6)
75. Basic Theory of Algebraic Groups and Lie Algebras, G. P. Hochschild (1981, ISBN 978-1-4613-8116-7)
76. Algebraic Geometry – An Introduction to Birational Geometry of Algebraic Varieties, Shigeru Iitaka (1982, ISBN 978-1-4613-8121-1)
77. Lectures on the Theory of Algebraic Numbers, E. T. Hecke (1981, ISBN 978-0-387-90595-2)
78. A Course in Universal Algebra, Burris, Stanley and Sankappanavar, H. P. (Online) (1981 ISBN 978-0-3879-0578-5)
79. An Introduction to Ergodic Theory, Peter Walters (1982, ISBN 978-0-387-95152-2)
80. A Course in the Theory of Groups, Derek J.S. Robinson [de] (1996, 2nd ed., ISBN 978-0-387-94461-6)
81. Lectures on Riemann Surfaces, Otto Forster (1981, ISBN 978-0-387-90617-1)
82. Differential Forms in Algebraic Topology, Raoul Bott, Loring W. Tu (1982, ISBN 978-0-387-90613-3)
83. Introduction to Cyclotomic Fields, Lawrence C. Washington (1997, 2nd ed., ISBN 978-0-387-94762-4)
84. A Classical Introduction to Modern Number Theory, Kenneth Ireland, Michael Rosen (1990, 2nd ed., ISBN 978-0-387-97329-6)
85. Fourier Series – A Modern Introduction Volume 2, R. E. Edwards (1982, 2nd ed., ISBN 978-1-4613-8158-7)
86. Introduction to Coding Theory, J. H. van Lint (3rd ed 1998, ISBN 3-540-64133-5)
87. Cohomology of Groups, Kenneth S. Brown (1982, ISBN 978-1-4684-9329-0)
88. Associative Algebras, R. S. Pierce (1982, ISBN 978-1-4757-0165-4)
89. Introduction to Algebraic and Abelian Functions, Serge Lang (1982, 2nd ed., ISBN 978-0-387-90710-9)
90. An Introduction to Convex Polytopes, Arne Brondsted (1983, ISBN 978-1-4612-1148-8)
91. The Geometry of Discrete Groups, Alan F. Beardon (1983, 2nd print 1995, ISBN 978-1-4612-7022-5)
92. Sequences and Series in Banach Spaces, J. Diestel (1984, ISBN 978-1-4612-9734-5)
93. Modern Geometry — Methods and Applications Part I: The Geometry of Surfaces, Transformation Groups, and Fields, B. A. Dubrovin, Anatoly Timofeevich Fomenko, Sergei Novikov (1992, 2nd ed., ISBN 978-0-387-97663-1)
94. Foundations of Differentiable Manifolds and Lie Groups, Frank W. Warner (1983, ISBN 978-0-387-90894-6)
95. Probability-1, Probability-2, Albert N. Shiryaev (2016, 2019, 3rd ed., ISBN 978-0-387-72205-4, ISBN 978-0-387-72207-8)
96. A Course in Functional Analysis, John B. Conway (2007, 2nd ed., ISBN 978-0-387-97245-9)
97. Introduction to Elliptic Curves and Modular Forms, Neal I. Koblitz (1993, 2nd ed., ISBN 978-0-387-97966-3)
98. Representations of Compact Lie Groups, Theodor Bröcker [de], Tammo tom Dieck (1985, ISBN 978-3-540-13678-1)
99. Finite Reflection Groups, L.C. Grove, C.T. Benson (1985, 2nd ed., ISBN 978-0-387-96082-1)
100. Harmonic Analysis on Semigroups – Theory of Positive Definite and Related Functions, Christian Berg, Jens Peter Reus Christensen, Paul Ressel (1984, ISBN 978-0-387-90925-7)
101. Galois Theory, Harold M. Edwards (1984, ISBN 978-0-387-90980-6)
102. Lie Groups, Lie Algebras, and Their Representations, V. S. Varadarajan (1984, ISBN 978-0-387-90969-1)
103. Complex Analysis, Serge Lang (1999, 4th ed., ISBN 978-0-387-98592-3)
104. Modern Geometry — Methods and Applications Part II: The Geometry and Topology of Manifolds, B. A. Dubrovin, Anatoly Timofeevich Fomenko, Sergei Novikov (1985, ISBN 978-0-387-96162-0)
105. SL2(R), Serge Lang (1985, ISBN 978-0-387-96198-9)
106. The Arithmetic of Elliptic Curves, Joseph H. Silverman (2009, 2nd ed., ISBN 978-0-387-09493-9)
107. Applications of Lie Groups to Differential Equations, Peter J. Olver (2ed 1993, ISBN 978-1-4684-0276-6)
108. Holomorphic Functions and Integral Representations in Several Complex Variables, R. Michael Range (1986, ISBN 978-0-387-96259-7)
109. Univalent Functions and Teichmüller Spaces, O. Lehto (1987, ISBN 978-1-4613-8654-4)
110. Algebraic Number Theory, Serge Lang (1994, 2nd ed., ISBN 978-0-387-94225-4)
111. Elliptic Curves, Dale Husemöller [de] (2004, 2nd ed., ISBN 978-0-387-95490-5)
112. Elliptic Functions, Serge Lang (1987, 2nd ed., ISBN 978-0-387-96508-6)
113. Brownian Motion and Stochastic Calculus, Ioannis Karatzas, Steven Shreve (2ed 2000, ISBN 978-0-387-97655-6)
114. A Course in Number Theory and Cryptography, Neal Koblitz (2ed 1994, ISBN 978-1-4684-0312-1)
115. Differential Geometry: Manifolds, Curves and Surfaces, Marcel Berger, Bernard Gostiaux (1988, ISBN 978-0-387-96626-7)
116. Measure and Integral — Volume 1, John L. Kelley, T.P. Srinivasan (1988, ISBN 978-0-387-96633-5)
117. Algebraic Groups and Class Fields, Jean-Pierre Serre (1988, ISBN 978-1-4612-6993-9)
118. Analysis Now, Gert K. Pedersen (1989, ISBN 978-0-387-96788-2)
119. An Introduction to Algebraic Topology, Joseph J. Rotman, (1988, ISBN 978-0-3879-6678-6)
120. Weakly Differentiable Functions — Sobolev Spaces and Functions of Bounded Variation, William P. Ziemer (1989, ISBN 978-0-387-97017-2)
121. Cyclotomic Fields I and II, Serge Lang (1990, Combined 2nd ed. ISBN 978-1-4612-6972-4)[3]
122. Theory of Complex Functions, Reinhold Remmert (1991, ISBN 978-0-387-97195-7)
123. Numbers, Heinz-Dieter Ebbinghaus et al. (1990, ISBN 978-0-387-97497-2)
124. Modern Geometry — Methods and Applications Part III: Introduction to Homology Theory, B. A. Dubrovin, Anatoly Timofeevich Fomenko, Sergei Novikov (1990, ISBN 978-0-387-97271-8)
125. Complex Variables — An Introduction, Carlos A. Berenstein, Roger Gay (1991, ISBN 978-0-387-97349-4)[4]
126. Linear Algebraic Groups, Armand Borel (1991, ISBN 978-1-4612-6954-0)
127. A Basic Course in Algebraic Topology, William S. Massey (1991, ISBN 978-0-3879-7430-9)
128. Partial Differential Equations, Jeffrey Rauch (1991, ISBN 978-1-4612-6959-5)
129. Representation Theory, William Fulton, Joe Harris (1991, ISBN 978-3-5400-0539-1)
130. Tensor Geometry — The Geometric Viewpoint and its Uses, Christopher T. J. Dodson, Timothy Poston (1991, 2nd ed., ISBN 978-3-540-52018-4)
131. A First Course in Noncommutative Rings, T. Y. Lam (2001, 2nd ed., ISBN 978-0-387-95183-6)
132. Iteration of Rational Functions — Complex Analytic Dynamical Systems, Alan F. Beardon (1991, ISBN 978-0-387-95151-5)
133. Algebraic Geometry, Joe Harris (1992, ISBN 978-0-387-97716-4)
134. Coding and Information Theory, Steven Roman (1992, ISBN 978-0-387-97812-3)
135. Advanced Linear Algebra, Steven Roman (2008, 3rd ed., ISBN 978-0-387-72828-5)
136. Algebra — An Approach via Module Theory, William Adkins, Steven Weintraub (1992, ISBN 978-0-387-97839-0)
137. Harmonic Function Theory, Sheldon Axler, Paul Bourdon, Wade Ramey (2001, 2nd ed., ISBN 978-0-387-95218-5)
138. A Course in Computational Algebraic Number Theory, Henri Cohen (1996, ISBN 0-387-55640-0)
139. Topology and Geometry, Glen E. Bredon (1993, ISBN 978-0-387-97926-7)
140. Optima and Equilibria, Jean-Pierre Aubin (1998, ISBN 978-3-642-08446-1)
141. Gröbner Bases — A Computational Approach to Commutative Algebra, Thomas Becker, Volker Weispfenning (1993, ISBN 978-0-387-97971-7)
142. Real and Functional Analysis, Serge Lang (1993, 3rd ed., ISBN 978-0-387-94001-4)
143. Measure Theory, J. L. Doob (1994, ISBN 978-0-387-94055-7)
144. Noncommutative Algebra, Benson Farb, R. Keith Dennis (1993, ISBN 978-0-387-94057-1)
145. Homology Theory — An Introduction to Algebraic Topology, James W. Vick (1994, 2nd ed., ISBN 978-0-387-94126-4)
146. Computability — A Mathematical Sketchbook, Douglas S. Bridges (1994, ISBN 978-0-387-94174-5)
147. Algebraic K-Theory and Its Applications, Jonathan Rosenberg (1994, ISBN 978-0-387-94248-3)
148. An Introduction to the Theory of Groups, Joseph J. Rotman (1995, 4th ed., ISBN 978-0-387-94285-8)
149. Foundations of Hyperbolic Manifolds, John G. Ratcliffe (2019, 3rd ed., ISBN 978-3-030-31597-9)
150. Commutative Algebra — with a View Toward Algebraic Geometry, David Eisenbud (1995, ISBN 978-0-387-94269-8)
151. Advanced Topics in the Arithmetic of Elliptic Curves, Joseph H. Silverman (1994, ISBN 978-0-387-94328-2)[5]
152. Lectures on Polytopes, Günter M. Ziegler (1995, ISBN 978-0-387-94365-7)
153. Algebraic Topology — A First Course, William Fulton (1995, ISBN 978-0-387-94327-5)
154. An Introduction to Analysis, Arlen Brown, Carl Pearcy (1995, ISBN 978-0-387-94369-5)
155. Quantum Groups, Christian Kassel (1995, ISBN 978-0-387-94370-1)
156. Classical Descriptive Set Theory, Alexander S. Kechris (1995, ISBN 978-0-387-94374-9)
157. Integration and Probability, Paul Malliavin (1995, ISBN 978-0-387-94409-8)[6]
158. Field Theory, Steven Roman (2006, 2nd ed., ISBN 978-0-387-27677-9)
159. Functions of One Complex Variable II, John B. Conway (1995, ISBN 978-0-387-94460-9)
160. Differential and Riemannian Manifolds, Serge Lang (1995, ISBN 978-0-387-94338-1)
161. Polynomials and Polynomial Inequalities, Peter Borwein, Tamas Erdelyi (1995, ISBN 978-0-387-94509-5)
162. Groups and Representations, J. L. Alperin, Rowen B. Bell (1995, ISBN 978-0-387-94526-2)
163. Permutation Groups, John D. Dixon, Brian Mortimer (1996, ISBN 978-0-387-94599-6)
164. Additive Number Theory The Classical Bases, Melvyn B. Nathanson (1996, ISBN 978-0-387-94656-6)
165. Additive Number Theory: Inverse Problems and the Geometry of Sumsets, Melvyn B. Nathanson (1996, ISBN 978-0-387-94655-9)
166. Differential Geometry — Cartan’s Generalization of Klein’s Erlangen Program, R. W. Sharpe (1997, ISBN 978-0-387-94732-7)
167. Field and Galois Theory, Patrick Morandi (1996, ISBN 978-0-387-94753-2)
168. Combinatorial Convexity and Algebraic Geometry, Guenter Ewald (1996, ISBN 978-1-4612-8476-5)
169. Matrix Analysis, Rajendra Bhatia (1997, ISBN 978-0-387-94846-1)
170. Sheaf Theory, Glen E. Bredon (1997, 2nd ed., ISBN 978-0-387-94905-5)
171. Riemannian Geometry, Peter Petersen (2016, 3rd ed., ISBN 978-3-319-26652-7)
172. Classical Topics in Complex Function Theory, Reinhold Remmert (1998, ISBN 978-0-387-98221-2)
173. Graph Theory, Reinhard Diestel [de] (2017, 5th ed., ISBN 978-3-662-53621-6)
174. Foundations of Real and Abstract Analysis, Douglas S. Bridges (1998, ISBN 978-0-387-98239-7)
175. An Introduction to Knot Theory, W. B. Raymond Lickorish (1997, ISBN 978-1-4612-6869-7)
176. Introduction to Riemannian Manifolds, John M. Lee (2018, 2nd ed., ISBN 978-3-319-91754-2)[7]
177. Analytic Number Theory , Donald J. Newman (1998, ISBN 978-0-387-98308-0)
178. Nonsmooth Analysis and Control Theory, Francis H. Clarke, Yuri S. Ledyaev, Ronald J. Stern, Peter R. Wolenski (1998, ISBN 978-0-387-98336-3)
179. Banach Algebra Techniques in Operator Theory, Ronald G. Douglas (1998, 2nd ed., ISBN 978-0-387-98377-6)
180. A Course on Borel Sets, S. M. Srivastava (1998, ISBN 978-0-387-98412-4)
181. Numerical Analysis, Rainer Kress (1998, ISBN 978-0-387-98408-7)
182. Ordinary Differential Equations, Wolfgang Walter (1998, ISBN 978-0-387-98459-9)
183. An Introduction to Banach Space Theory, Robert E. Megginson (1998, ISBN 978-0-387-98431-5)
184. Modern Graph Theory, Béla Bollobás (1998, ISBN 978-0-387-98488-9)
185. Using Algebraic Geometry, David A. Cox, John Little, Donal O’Shea (2005, 2nd ed., ISBN 978-0-387-20706-3)
186. Fourier Analysis on Number Fields, Dinakar Ramakrishnan, Robert J. Valenza (1999, ISBN 978-0-387-98436-0)
187. Moduli of Curves, Joe Harris, Ian Morrison (1998, ISBN 978-0-387-98438-4)
188. Lectures on the Hyperreals – An Introduction to Nonstandard Analysis, Robert Goldblatt (1998, ISBN 978-0-387-98464-3)
189. Lectures on Modules and Rings, Tsit-Yuen Lam (1999, ISBN 978-0-387-98428-5)
190. Problems in Algebraic Number Theory, M. Ram Murty, Jody Indigo Esmonde (2005, 2nd ed., ISBN 978-0-387-22182-3)
191. Fundamentals of Differential Geometry, Serge Lang (1999, ISBN 978-0-387-98593-0)
192. Elements of Functional Analysis, Francis Hirsch, Gilles Lacombe (1999, ISBN 978-0-387-98524-4)
193. Advanced Topics in Computational Number Theory, Henri Cohen (2000, ISBN 0-387-98727-4)
194. One-Parameter Semigroups for Linear Evolution Equations, Klaus-Jochen Engel, Rainer Nagel (2000, ISBN 978-0-387-98463-6)
195. Elementary Methods in Number Theory, Melvyn B. Nathanson (2000, ISBN 978-0-387-98912-9)
196. Basic Homological Algebra, M. Scott Osborne (2000, ISBN 978-0-387-98934-1)
197. The Geometry of Schemes, Eisenbud, Joe Harris (2000, ISBN 978-0-387-98638-8)
198. A Course in p-adic Analysis, Alain M. Robert (2000, ISBN 978-0-387-98669-2)
199. Theory of Bergman Spaces, Hakan Hedenmalm, Boris Korenblum, Kehe Zhu (2000, ISBN 978-0-387-98791-0)
200. An Introduction to Riemann–Finsler Geometry, David Bao, Shiing-Shen Chern, Zhongmin Shen (2000, ISBN 978-1-4612-7070-6)
201. Diophantine Geometry, Marc Hindry, Joseph H. Silverman (2000, ISBN 978-0-387-98975-4)
202. Introduction to Topological Manifolds, John M. Lee (2011, 2nd ed., ISBN 978-1-4419-7939-1)
203. The Symmetric Group — Representations, Combinatorial Algorithms, and Symmetric Functions, Bruce E. Sagan (2001, 2nd ed., ISBN 978-0-387-95067-9)
204. Galois Theory, Jean-Pierre Escofier (2001, ISBN 978-0-387-98765-1)
205. Rational Homotopy Theory, Yves Félix, Stephen Halperin, Jean-Claude Thomas (2000, ISBN 978-0-387-95068-6)
206. Problems in Analytic Number Theory, M. Ram Murty (2007, 2nd ed., ISBN 978-0-387-95143-0)
207. Algebraic Graph Theory, Chris Godsil, Gordon Royle (2001, ISBN 978-0-387-95241-3)
208. Analysis for Applied Mathematics, Ward Cheney (2001, ISBN 978-0-387-95279-6)
209. A Short Course on Spectral Theory, William Arveson (2002, ISBN 978-0-387-95300-7)
210. Number Theory in Function Fields, Michael Rosen (2002, ISBN 978-0-387-95335-9)
211. Algebra, Serge Lang (2002, Revised 3rd ed, ISBN 978-0-387-95385-4)
212. Lectures on Discrete Geometry, Jiří Matoušek (2002, ISBN 978-0-387-95374-8)
213. From Holomorphic Functions to Complex Manifolds, Klaus Fritzsche [de], Hans Grauert (2002, ISBN 978-0-387-95395-3)
214. Partial Differential Equations, Jürgen Jost, (2013, 3rd ed., ISBN 978-1-4614-4808-2)
215. Algebraic Functions and Projective Curves, David M. Goldschmidt, (2003, ISBN 978-0-387-95432-5)
216. Matrices — Theory and Applications, Denis Serre, (2010, 2nd ed., ISBN 978-1-4419-7682-6)
217. Model Theory: An Introduction, David Marker, (2002, ISBN 978-0-387-98760-6)
218. Introduction to Smooth Manifolds, John M. Lee (2012, 2nd ed., ISBN 978-1-4419-9981-8)
219. The Arithmetic of Hyperbolic 3-Manifolds, Colin Maclachlan, Alan W. Reid, (2003, ISBN 978-0-387-98386-8)
220. Smooth Manifolds and Observables, Jet Nestruev, (2020, 2nd ed., ISBN 978-0-387-95543-8 )
221. Convex Polytopes, Branko Grünbaum (2003, 2nd ed., ISBN 978-0-387-40409-7)
222. Lie Groups, Lie Algebras, and Representations – An Elementary Introduction, Brian C. Hall, (2015, 2nd ed., ISBN 978-3-319-13466-6)
223. Fourier Analysis and its Applications, Anders Vretblad, (2003, ISBN 978-0-387-00836-3)
224. Metric Structures in Differential Geometry, Walschap, G., (2004, ISBN 978-0-387-20430-7)
225. Lie Groups, Daniel Bump, (2013, 2nd ed., ISBN 978-1-4614-8023-5)
226. Spaces of Holomorphic Functions in the Unit Ball, Kehe Zhu, (2005, ISBN 978-0-387-22036-9)
227. Combinatorial Commutative Algebra, Ezra Miller, Bernd Sturmfels, (2005, ISBN 978-0-387-22356-8)
228. A First Course in Modular Forms, Fred Diamond, J. Shurman, (2006, ISBN 978-0-387-23229-4)
229. The Geometry of Syzygies – A Second Course in Algebraic Geometry and Commutative Algebra, David Eisenbud (2005, ISBN 978-0-387-22215-8)
230. An Introduction to Markov Processes, Daniel W. Stroock, (2014, 2nd ed., ISBN 978-3-540-23499-9)
231. Combinatorics of Coxeter Groups, Anders Björner, Francisco Brenti, (2005, ISBN 978-3-540-44238-7)
232. An Introduction to Number Theory, Everest, Graham., Ward, T., (2005, ISBN 978-1-85233-917-3)
233. Topics in Banach Space Theory, Albiac, F., Kalton, N. J., (2016, 2nd ed., ISBN 978-3-319-31555-3)
234. Analysis and Probability — Wavelets, Signals, Fractals, Jorgensen, P. E. T., (2006, ISBN 978-0-387-29519-0)
235. Compact Lie Groups, M. R. Sepanski, (2007, ISBN 978-0-387-30263-8)
236. Bounded Analytic Functions, Garnett, J., (2007, ISBN 978-0-387-33621-3)
237. An Introduction to Operators on the Hardy–Hilbert Space, Ruben A. Martinez-Avendano, Peter Rosenthal, (2007, ISBN 978-0-387-35418-7)
238. A Course in Enumeration, Martin Aigner, (2007, ISBN 978-3-540-39032-9)
239. Number Theory — Volume I: Tools and Diophantine Equations, Henri Cohen, (2007, ISBN 978-0-387-49922-2)
240. Number Theory — Volume II: Analytic and Modern Tools, Henri Cohen, (2007, ISBN 978-0-387-49893-5)
241. The Arithmetic of Dynamical Systems, Joseph H. Silverman, (2007, ISBN 978-0-387-69903-5)
242. Abstract Algebra, Grillet, Pierre Antoine, (2007, ISBN 978-0-387-71567-4)
243. Topological Methods in Group Theory, Geoghegan, Ross, (2007, ISBN 978-0-387-74611-1)
244. Graph Theory, Adrian Bondy, U.S.R. Murty, (2008, ISBN 978-1-84628-969-9)
245. Complex Analysis – In the Spirit of Lipman Bers, Rubí E. Rodríguez, Irwin Kra, Jane P. Gilman (2013, 2nd ed., ISBN 978-1-4899-9908-5)
246. A Course in Commutative Banach Algebras, Kaniuth, Eberhard, (2008, ISBN 978-0-387-72475-1)
247. Braid Groups, Kassel, Christian, Turaev, Vladimir, (2008, ISBN 978-0-387-33841-5)
248. Buildings Theory and Applications, Abramenko, Peter, Brown, Ken (2008, ISBN 978-0-387-78834-0)
249. Classical Fourier Analysis, Loukas Grafakos (2014, 3rd ed., ISBN 978-1-4939-1193-6)
250. Modern Fourier Analysis, Loukas Grafakos (2014, 3rd ed., ISBN 978-1-4939-1229-2)
251. The Finite Simple Groups, Robert A. Wilson (2009, ISBN 978-1-84800-987-5)
252. Distributions and Operators, Gerd Grubb, (2009, ISBN 978-0-387-84894-5)
253. Elementary Functional Analysis, MacCluer, Barbara D., (2009, ISBN 978-0-387-85528-8)
254. Algebraic Function Fields and Codes, Henning Stichtenoth [de], (2009, 2nd ed., ISBN 978-3-540-76877-7)
255. Symmetry, Representations, and Invariants, Goodman, Roe, Wallach, Nolan R., (2009, ISBN 978-0-387-79851-6)
256. A Course in Commutative Algebra, Kemper, Gregor, (2010, ISBN 978-3-642-03544-9)
257. Deformation Theory, Robin Hartshorne, (2010, ISBN 978-1-4419-1595-5)
258. Foundations of Optimization in Finite Dimensions, Osman Guler, (2010, ISBN 978-0-387-34431-7)
259. Ergodic Theory – with a view towards Number Theory, Thomas Ward, Manfred Einsiedler, (2011, ISBN 978-0-85729-020-5)
260. Monomial Ideals, Jürgen Herzog, Hibi Takayuki(2010, ISBN 978-0-85729-105-9)
261. Probability and Stochastics, Erhan Cinlar, (2011, ISBN 978-0-387-87858-4)
262. Essentials of Integration Theory for Analysis, Daniel W. Stroock, (2012, ISBN 978-1-4614-1134-5)
263. Analysis on Fock Spaces, Kehe Zhu, (2012, ISBN 978-1-4419-8800-3)
264. Functional Analysis, Calculus of Variations and Optimal Control, Francis H. Clarke, (2013, ISBN 978-1-4471-4819-7)
265. Unbounded Self-adjoint Operators on Hilbert Space, Konrad Schmüdgen, (2012, ISBN 978-94-007-4752-4)
266. Calculus Without Derivatives, Jean-Paul Penot, (2012, ISBN 978-1-4614-4537-1)
267. Quantum Theory for Mathematicians, Brian C. Hall, (2013, ISBN 978-1-4614-7115-8)
268. Geometric Analysis of the Bergman Kernel and Metric, Krantz, Steven G., (2013, ISBN 978-1-4614-7923-9)
269. Locally Convex Spaces, M Scott Osborne, (2014, ISBN 978-3-319-02044-0)
270. Fundamentals of Algebraic Topology, Steven Weintraub, (2014, ISBN 978-1-4939-1843-0)
271. Integer Programming, Michelangelo Conforti, Gérard P. Cornuéjols, Giacomo Zambelli, (2014, ISBN 978-3-319-11007-3)
272. Operator Theoretic Aspects of Ergodic Theory, Tanja Eisner, Bálint Farkas, Markus Haase, Rainer Nagel, (2015, ISBN 978-3-319-16897-5)
273. Homotopical Topology, Anatoly Fomenko, Dmitry Fuchs, (2016, 2nd ed., ISBN 978-3-319-23487-8)
274. Brownian Motion, Martingales, and Stochastic Calculus, Jean-François Le Gall, (2016, ISBN 978-3-319-31088-6)
275. Differential Geometry – Connections, Curvature, and Characteristic Classes, Loring W. Tu (2017, ISBN 978-3-319-55082-4)
276. Functional Analysis, Spectral Theory, and Applications, Manfred Einsiedler, Thomas Ward (2017, ISBN 978-3-319-58539-0)
277. The Moment Problem, Konrad Schmüdgen (2017, ISBN 978-3-319-64545-2)
278. Modern Real Analysis, William P. Ziemer (2017, 2nd ed., ISBN 978-3-319-64628-2)
279. Binomial Ideals, Jürgen Herzog, Takayuki Hibi, Hidefumi Ohsugi (2018, ISBN 978-3-319-95347-2)
280. Introduction to Real Analysis, Christopher Heil (2019, ISBN 978-3-030-26901-2)
281. Intersection Homology & Perverse Sheaves with Applications to Singularities, Laurenţiu G. Maxim (2019, ISBN 978-3-030-27644-7)
282. Measure, Integration & Real Analysis, Sheldon Axler (2020, ISBN 978-3-030-33143-6)
283. Basic Representation Theory of Algebras, Ibrahim Assem, Flávio U Coelho (2020, ISBN 978-3-030-35117-5)
284. Spectral Theory – Basic Concepts and Applications, David Borthwick (2020, ISBN 978-3-030-38001-4)
285. An Invitation to Unbounded Representations of ∗-Algebras on Hilbert Space, Konrad Schmüdgen (2020, ISBN 978-3-030-46365-6)
286. Lectures on Convex Geometry, Daniel Hug, Wolfgang Weilt (2020, ISBN 978-3-030-50179-2)
287. Explorations in Complex Functions, Richard Beals, Roderick S. C. Wong (2020, ISBN 978-3-030-54532-1)
288. Quaternion Algebras, John Voight (2020, ISBN 978-3-030-56692-0)
289. Ergodic Dynamics – From Basic Theory to Applications, Jane M. Hawkins (2020, ISBN 978-3-030-59242-4)
290. Lessons in Enumerative Combinatorics, Omer Egecioglu , Adriano Garsia (2021, ISBN 978-3-030-71249-5)
291. Mathematical Logic, Heinz-Dieter Ebbinghaus, Jörg Flum, Wolfgang Thomas (2021, 3rd ed. ISBN 978-3-030-73839-6)
292. Random Walk, Brownian Motion and Martingales, Rabi Bhattacharya, Edward C. Waymire (2021, ISBN 978-3-030-78939-8)

---

Graduate Studies in Mathematics

List of books[edit]

• 1 The General Topology of Dynamical Systems, Ethan Akin (1993, ISBN 978-0-8218-4932-3)[1]
• 2 Combinatorial Rigidity, Jack Graver, Brigitte Servatius, Herman Servatius (1993, ISBN 978-0-8218-3801-3)
• 3 An Introduction to Gröbner Bases, William W. Adams, Philippe Loustaunau (1994, ISBN 978-0-8218-3804-4)
• 4 The Integrals of Lebesgue, Denjoy, Perron, and Henstock, Russell A. Gordon (1994, ISBN 978-0-8218-3805-1)
• 5 Algebraic Curves and Riemann Surfaces, Rick Miranda (1995, ISBN 978-0-8218-0268-7)
• 6 Lectures on Quantum Groups, Jens Carsten Jantzen (1996, ISBN 978-0-8218-0478-0)
• 7 Algebraic Number Fields, Gerald J. Janusz (1996, 2nd ed., ISBN 978-0-8218-0429-2)
• 8 Discovering Modern Set Theory. I: The Basics, Winfried Just, Martin Weese (1996, ISBN 978-0-8218-0266-3)
• 9 An Invitation to Arithmetic Geometry, Dino Lorenzini (1996, ISBN 978-0-8218-0267-0)
• 10 Representations of Finite and Compact Groups, Barry Simon (1996, ISBN 978-0-8218-0453-7)
• 11 Enveloping Algebras, Jacques Dixmier (1996, ISBN 978-0-8218-0560-2)
• 12 Lectures on Elliptic and Parabolic Equations in Hölder Spaces, N. V. Krylov (1996, ISBN 978-0-8218-0569-5)
• 13 The Ergodic Theory of Discrete Sample Paths, Paul C. Shields (1996, ISBN 978-0-8218-0477-3)
• 14 Analysis, Elliott H. Lieb, Michael Loss (2001, 2nd ed., ISBN 978-0-8218-2783-3)
• 15 Fundamentals of the Theory of Operator Algebras. Volume I: Elementary Theory, Richard V. Kadison, John R. Ringrose (1997, ISBN 978-0-8218-0819-1)[2]
• 16 Fundamentals of the Theory of Operator Algebras. Volume II: Advanced Theory, Richard V. Kadison, John R. Ringrose (1997, ISBN 978-0-8218-0820-7)[3]
• 17 Topics in Classical Automorphic Forms, Henryk Iwaniec (1997, ISBN 978-0-8218-0777-4)
• 18 Discovering Modern Set Theory. II: Set-Theoretic Tools for Every Mathematician, Winfried Just, Martin Weese (1997, ISBN 978-0-8218-0528-2)
• 19 Partial Differential Equations, Lawrence C. Evans (2010, 2nd ed., ISBN 978-0-8218-4974-3)
• 20 4-Manifolds and Kirby Calculus, Robert E. Gompf, András I. Stipsicz (1999, ISBN 978-0-8218-0994-5)
• 21 A Course in Operator Theory, John B. Conway (2000, ISBN 978-0-8218-2065-0)
• 22 Growth of Algebras and Gelfand-Kirillov Dimension, Günter R. Krause, Thomas H. Lenagan (2000, Revised ed., ISBN 978-0-8218-0859-7)
• 23 Foliations I, Alberto Candel, Lawrence Conlon (2000, ISBN 978-0-8218-0809-2)
• 24 Number Theory: Algebraic Numbers and Functions, Helmut Koch (2000, ISBN 978-0-8218-2054-4)
• 25 Dirac Operators in Riemannian Geometry, Thomas Friedrich (2000, ISBN 978-0-8218-2055-1)
• 26 An Introduction to Symplectic Geometry, Rolf Berndt (2001, ISBN 978-0-8218-2056-8)
• 27 A Course in Differential Geometry, Thierry Aubin (2001, ISBN 978-0-8218-2709-3)
• 28 Notes on Seiberg-Witten Theory, Liviu I. Nicolaescu (2000, ISBN 978-0-8218-2145-9)
• 29 Fourier Analysis, Javier Duoandikoetxea (2001, ISBN 978-0-8218-2172-5)
• 30 Noncommutative Noetherian Rings, J. C. McConnell, J. C. Robson (1987, ISBN 978-0-8218-2169-5); 2001 pbk reprint with corrections
• 31 Option Pricing and Portfolio Optimization: Modern Methods of Financial Mathematics, Ralf Korn, Elke Korn (2001, ISBN 978-0-8218-2123-7)
• 32 A Modern Theory of Integration, Robert G. Bartle (2001, ISBN 978-0-8218-0845-0)[4]
• 33 A Course in Metric Geometry, Dmitri Burago, Yuri Burago, Sergei Ivanov (2001, ISBN 978-0-8218-2129-9)
• 34 Differential Geometry, Lie Groups, and Symmetric Spaces, Sigurdur Helgason (2001, ISBN 978-0-8218-2848-9)
• 35 Lecture Notes in Algebraic Topology, James F. Davis, Paul Kirk (2001, ISBN 978-0-8218-2160-2)
• 36 Principles of Functional Analysis, Martin Schechter (2002, 2nd ed., ISBN 978-0-8218-2895-3)
• 37 Theta Constants, Riemann Surfaces and the Modular Group: An Introduction with Applications to Uniformization Theorems, Partition Identities and Combinatorial Number Theory, Hershel M. Farkas, Irwin Kra (2001, ISBN 978-0-8218-1392-8)
• 38 Stochastic Analysis on Manifolds, Elton P. Hsu (2002, ISBN 978-0-8218-0802-3)
• 39 Classical Groups and Geometric Algebra, Larry C. Grove (2002, ISBN 978-0-8218-2019-3)
• 40 Function Theory of One Complex Variable, Robert E. Greene, Steven G. Krantz (2006, 3rd ed., ISBN 978-0-8218-3962-1)
• 41 Introduction to the Theory of Differential Inclusions, Georgi V. Smirnov (2002, ISBN 978-0-8218-2977-6)
• 42 Introduction to Quantum Groups and Crystal Bases, Jin Hong, Seok-Jin Kang (2002, ISBN 978-0-8218-2874-8)
• 43 Introduction to the Theory of Random Processes, N. V. Krylov (2002, ISBN 978-0-8218-2985-1)
• 44 Pick Interpolation and Hilbert Function Spaces, Jim Agler, John E. McCarthy (2002, ISBN 978-0-8218-2898-4)
• 45 An Introduction to Measure and Integration, Inder K. Rana (2002, 2nd ed., ISBN 978-0-8218-2974-5)
• 46 Several Complex Variables with Connections to Algebraic Geometry and Lie Groups, Joseph L. Taylor (2002, ISBN 978-0-8218-3178-6)
• 47 Classical and Quantum Computation, A. Yu. Kitaev, A. H. Shen, M. N. Vyalyi (2002, ISBN 978-0-8218-3229-5)[5]
• 48 Introduction to the h-Principle, Y. Eliashberg, N. Mishachev (2002, ISBN 978-0-8218-3227-1)
• 49 Secondary Cohomology Operations, John R. Harper (2002, ISBN 978-0-8218-3270-7)
• 50 An Invitation to Operator Theory, Y. A. Abramovich, C. D. Aliprantis (2002, ISBN 978-0-8218-2146-6)[6]
• 51 Problems in Operator Theory, Y. A. Abramovich, C. D. Aliprantis (2002, ISBN 978-0-8218-2147-3)[6]
• 52 Global Analysis: Differential Forms in Analysis, Geometry and Physics, Ilka Agricola, Thomas Friedrich (2002, ISBN 978-0-8218-2951-6)
• 53 Spectral Methods of Automorphic Forms, Henryk Iwaniec (2002, 2nd ed., ISBN 978-0-8218-3160-1)
• 54 A Course in Convexity, Alexander Barvinok (2002, ISBN 978-0-8218-2968-4)
• 55 A Scrapbook of Complex Curve Theory, C. Herbert Clemens (2003, 2nd ed., ISBN 978-0-8218-3307-0)
• 56 A Course in Algebra, E. B. Vinberg (2003, ISBN 978-0-8218-3318-6)
• 57 Concise Numerical Mathematics, Robert Plato (2003, ISBN 978-0-8218-2953-0)
• 58 Topics in Optimal Transportation, Cédric Villani (2003, ISBN 978-0-8218-3312-4)
• 59 Representation Theory of Finite Groups: Algebra and Arithmetic, Steven H. Weintraub (2003, ISBN 978-0-8218-3222-6)
• 60 Foliations II, Alberto Candel, Lawrence Conlon (2003, ISBN 978-0-8218-0881-8)
• 61 Cartan for Beginners: Differential Geometry via Moving Frames and Exterior Differential Systems, Thomas A. Ivey, J. M. Landsberg (2003, ISBN 978-0-8218-3375-9)[7]
• 62 A Companion to Analysis: A Second First and First Second Course in Analysis, T. W. Körner (2004, ISBN 978-0-8218-3447-3)
• 63 Resolution of Singularities, Steven Dale Cutkosky (2004, ISBN 978-0-8218-3555-5)
• 64 Lectures on the Orbit Method, A. A. Kirillov (2004, ISBN 978-0-8218-3530-2)
• 65 Global Calculus, S. Ramanan (2005, ISBN 978-0-8218-3702-3)
• 66 Functional Analysis: An Introduction, Yuli Eidelman, Vitali Milman, Antonis Tsolomitis (2004, ISBN 978-0-8218-3646-0)
• 67 Introduction to Quadratic Forms over Fields, T.Y. Lam (2005, ISBN 978-0-8218-1095-8)
• 68 A Geometric Approach to Free Boundary Problems, Luis Caffarelli, Sandro Salsa (2005, ISBN 978-0-8218-3784-9)
• 69 Curves and Surfaces, Sebastián Montiel, Antonio Ros (2009, 2nd ed., ISBN 978-0-8218-4763-3)
• 70 Probability Theory in Finance: A Mathematical Guide to the Black-Scholes Formula, Seán Dineen (2013, 2nd ed., ISBN 978-0-8218-9490-3)
• 71 Modern Geometric Structures and Fields, S. P. Novikov, I. A. Taimanov (2006, ISBN 978-0-8218-3929-4)
• 72 Introduction to the Mathematics of Finance, Ruth J. Williams (2006, ISBN 978-0-8218-3903-4)
• 73 Graduate Algebra: Commutative View, Louis Halle Rowen (2006, ISBN 978-0-8218-0570-1)
• 74 Elements of Combinatorial and Differential Topology, V. V. Prasolov (2006, ISBN 978-0-8218-3809-9)
• 75 Applied Asymptotic Analysis, Peter D. Miller (2006, ISBN 978-0-8218-4078-8)
• 76 Measure Theory and Integration, Michael E. Taylor (2006, ISBN 978-0-8218-4180-8)
• 77 Hamilton’s Ricci Flow, Bennett Chow, Peng Lu, Lei Ni (2006, ISBN 978-0-8218-4231-7)
• 78 Linear Algebra in Action, Harry Dym (2013, 2nd ed., ISBN 978-1-4704-0908-1)
• 79 Modular Forms, a Computational Approach, William A. Stein (2007, ISBN 978-0-8218-3960-7)
• 80 Probability, Davar Khoshnevisan (2007, ISBN 978-0-8218-4215-7)
• 81 Elements of Homology Theory, V. V. Prasolov (2007, ISBN 978-0-8218-3812-9)[8]
• 82 Pseudo-differential Operators and the Nash-Moser Theorem, Serge Alinhac, Patrick Gérard (2007, ISBN 978-0-8218-3454-1)
• 83 Functions of Several Complex Variables and Their Singularities, Wolfgang Ebeling (2007, ISBN 978-0-8218-3319-3)
• 84 Cones and Duality, Charalambos D. Aliprantis, Rabee Tourky (2007, ISBN 978-0-8218-4146-4)
• 85 Recurrence and Topology, John M. Alongi, Gail S. Nelson (2007, ISBN 978-0-8218-4234-8)
• 86 Lectures on Analytic Differential Equations, Yulij Ilyashenko, Sergei Yakovenko (2008, ISBN 978-0-8218-3667-5)
• 87 Twenty-Four Hours of Local Cohomology, Srikanth B. Iyengar, Graham J. Leuschke, Anton Leykin, Claudia Miller, Ezra Miller, Anurag K. Singh, Uli Walther (2007, ISBN 978-0-8218-4126-6)
• 88 C∗-Algebras and Finite-Dimensional Approximations, Nathanial P. Brown, Narutaka Ozawa (2008, ISBN 978-0-8218-4381-9)
• 89 A Course on the Web Graph, Anthony Bonato (2008, ISBN 978-0-8218-4467-0)
• 90 Basic Quadratic Forms, Larry J. Gerstein (2008, ISBN 978-0-8218-4465-6)
• 91 Graduate Algebra: Noncommutative View, Louis Halle Rowen (2008, ISBN 978-0-8218-4153-2)[9]
• 92 Finite Group Theory, I. Martin Isaacs (2008, ISBN 978-0-8218-4344-4)
• 93 Topics in Differential Geometry, Peter W. Michor (2008, ISBN 978-0-8218-2003-2)
• 94 Representations of Semisimple Lie Algebras in the BGG Category O, James E. Humphreys (2008, ISBN 978-0-8218-4678-0)
• 95 Quantum Mechanics for Mathematicians, Leon A. Takhtajan (2008, ISBN 978-0-8218-4630-8)
• 96 Lectures on Elliptic and Parabolic Equations in Sobolev Spaces, N. V. Krylov (2008, ISBN 978-0-8218-4684-1)
• 97 Complex Made Simple, David C. Ullrich (2008, ISBN 978-0-8218-4479-3)
• 98 Discrete Differential Geometry: Integrable Structure, Alexander I. Bobenko, Yuri B. Suris (2008, ISBN 978-0-8218-4700-8)
• 99 Mathematical Methods in Quantum Mechanics: With Applications to Schrödinger Operators, Gerald Teschl (2009, ISBN 978-0-8218-4660-5)[10]
• 100 Algebra: A Graduate Course, I. Martin Isaacs (1994, ISBN 978-0-8218-4799-2)
• 101 A Course in Approximation Theory, Ward Cheney, Will Light (2000, ISBN 978-0-8218-4798-5)
• 102 Introduction to Fourier Analysis and Wavelets, Mark A. Pinsky (2002, ISBN 978-0-8218-4797-8)
• 103 Configurations of Points and Lines, Branko Grünbaum (2009, ISBN 978-0-8218-4308-6)
• 104 Algebra: Chapter 0, Paolo Aluffi (2009, ISBN 978-0-8218-4781-7)
• 105 A First Course in Sobolev Spaces, Giovanni Leoni (2009, ISBN 978-0-8218-4768-8)[11]
• 106 Embeddings in Manifolds, Robert J. Daverman, Gerard A. Venema (2009, ISBN 978-0-8218-3697-2)
• 107 Manifolds and Differential Geometry, Jeffrey M. Lee (2009, ISBN 978-0-8218-4815-9)
• 108 Mapping Degree Theory, Enrique Outerelo, Jesús M. Ruiz (2009, ISBN 978-0-8218-4915-6)
• 109 Training Manual on Transport and Fluids, John C. Neu (2010, ISBN 978-0-8218-4083-2)
• 110 Differential Algebraic Topology: From Stratifolds to Exotic Spheres, Matthias Kreck (2010, ISBN 978-0-8218-4898-2)
• 111 Ricci Flow and the Sphere Theorem, Simon Brendle (2010, ISBN 978-0-8218-4938-5)
• 112 Optimal Control of Partial Differential Equations: Theory, Methods and Applications, Fredi Troltzsch (2010, ISBN 978-0-8218-4904-0)
• 113 Continuous Time Markov Processes: An Introduction, Thomas M. Liggett (2010, ISBN 978-0-8218-4949-1)
• 114 Advanced Modern Algebra, Joseph J. Rotman (2010, 2nd ed., ISBN 978-0-8218-4741-1)[12]
• 115 An Introductory Course on Mathematical Game Theory, Julio González-Díaz, Ignacio García-Jurado, M. Gloria Fiestras-Janeiro (2010, ISBN 978-0-8218-5151-7)
• 116 Linear Functional Analysis, Joan Cerdà (2010, ISBN 978-0-8218-5115-9)
• 117 An Epsilon of Room, I: Real Analysis: pages from year three of a mathematical blog, Terence Tao (2010, ISBN 978-0-8218-5278-1)
• 118 Dynamical Systems and Population Persistence, Hal L. Smith, Horst R. Thieme (2011, ISBN 978-0-8218-4945-3)
• 119 Mathematical Statistics: Asymptotic Minimax Theory, Alexander Korostelev, Olga Korosteleva (2011, ISBN 978-0-8218-5283-5)
• 120 A Basic Course in Partial Differential Equations, Qing Han (2011, ISBN 978-0-8218-5255-2)
• 121 A Course in Minimal Surfaces, Tobias Holck Colding, William P. Minicozzi II (2011, ISBN 978-0-8218-5323-8)
• 122 Algebraic Groups and Differential Galois Theory, Teresa Crespo, Zbigniew Hajto (2011, ISBN 978-0-8218-5318-4)
• 123 Lectures on Linear Partial Differential Equations, Gregory Eskin (2011, ISBN 978-0-8218-5284-2)
• 124 Toric Varieties, David A. Cox, John B. Little, Henry K. Schenck (2011, ISBN 978-0-8218-4819-7)
• 125 Riemann Surfaces by Way of Complex Analytic Geometry, Dror Varolin (2011, ISBN 978-0-8218-5369-6)
• 126 An Introduction to Measure Theory, Terence Tao (2011, ISBN 978-0-8218-6919-2)
• 127 Modern Classical Homotopy Theory, Jeffrey Strom (2011, ISBN 978-0-8218-5286-6)
• 128 Tensors: Geometry and Applications, J. M. Landsberg (2012, ISBN 978-0-8218-6907-9)
• 129 Classical Methods in Ordinary Differential Equations: With Applications to Boundary Value Problems, Stuart P. Hastings, J. Bryce McLeod (2012, ISBN 978-0-8218-4694-0)
• 130 Gröbner Bases in Commutative Algebra, Viviana Ene, Jürgen Herzog (2011, ISBN 978-0-8218-7287-1)
• 131 Lie Superalgebras and Enveloping Algebras, Ian M. Musson (2012, ISBN 978-0-8218-6867-6)
• 132 Topics in Random Matrix Theory, Terence Tao (2012, ISBN 978-0-8218-7430-1)
• 133 Hyperbolic Partial Differential Equations and Geometric Optics, Jeffrey Rauch (2012, ISBN 978-0-8218-7291-8)
• 134 Analytic Number Theory: Exploring the Anatomy of Integers, Jean-Marie De Koninck, Florian Luca (2012, ISBN 978-0-8218-7577-3)
• 135 Linear and Quasi-linear Evolution Equations in Hilbert Spaces, Pascal Cherrier, Albert Milani (2012, ISBN 978-0-8218-7576-6)
• 136 Regularity of Free Boundaries in Obstacle-Type Problems, Arshak Petrosyan, Henrik Shahgholian, Nina Uraltseva (2012, ISBN 978-0-8218-8794-3)
• 137 Ordinary Differential Equations: Qualitative Theory, Luis Barreira, Clàudia Valls (2012, ISBN 978-0-8218-8749-3)
• 138 Semiclassical Analysis, Maciej Zworski (2012, ISBN 978-0-8218-8320-4)
• 139 Knowing the Odds: An Introduction to Probability, John B. Walsh (2012, ISBN 978-0-8218-8532-1)
• 140 Ordinary Differential Equations and Dynamical Systems, Gerald Teschl (2012, ISBN 978-0-8218-8328-0)
• 141 A Course in Abstract Analysis, John B. Conway (2012, ISBN 978-0-8218-9083-7)
• 142 Higher Order Fourier Analysis, Terence Tao (2012, ISBN 978-0-8218-8986-2)
• 143 Lecture Notes on Functional Analysis: With Applications to Linear Partial Differential Equations, Alberto Bressan (2013, ISBN 978-0-8218-8771-4)
• 144 Dualities and Representations of Lie Superalgebras, Shun-Jen Cheng, Weiqiang Wang (2012, ISBN 978-0-8218-9118-6)
• 145 The K-book: An Introduction to Algebraic K-theory, Charles A. Weibel (2013, ISBN 978-0-8218-9132-2)
• 146 Combinatorial Game Theory, Aaron N. Siegel (2013, ISBN 978-0-8218-5190-6)
• 147 Matrix Theory, Xingzhi Zhan (2013, ISBN 978-0-8218-9491-0)
• 148 Introduction to Smooth Ergodic Theory, Luis Barreira, Yakov Pesin (2013, ISBN 978-0-8218-9853-6)
• 149 Mathematics of Probability, Daniel W. Stroock (2013, ISBN 978-1-4704-0907-4)
• 150 The Joys of Haar Measure, Joe Diestel, Angela Spalsbury (2013, ISBN 978-1-4704-0935-7)
• 151 Introduction to 3-Manifolds, Jennifer Schultens (2014, ISBN 978-1-4704-1020-9)
• 152 An Introduction to Extremal Kähler Metrics, Gábor Székelyhidi (2014, ISBN 978-1-4704-1047-6)
• 153 Hilbert’s Fifth Problem and Related Topics, Terence Tao (2014, ISBN 978-1-4704-1564-8)
• 154 A Course in Complex Analysis and Riemann Surfaces, Wilhelm Schlag (2014, ISBN 978-0-8218-9847-5)
• 155 An Introduction to the Representation Theory of Groups, Emmanuel Kowalski (2014, ISBN 978-1-4704-0966-1)
• 156 Functional Analysis: An Elementary Introduction, Markus Haase (2014, ISBN 978-0-8218-9171-1)
• 157 Mathematical Methods in Quantum Mechanics: With Applications to Schrödinger Operators, Gerald Teschl (2014, 2nd ed., ISBN 978-1-4704-1704-8)
• 158 Dynamical Systems and Linear Algebra, Fritz Colonius, Wolfgang Kliemann (2014, ISBN 978-0-8218-8319-8)
• 159 The Role of Nonassociative Algebra in Projective Geometry, John R. Faulkner (2014, ISBN 978-1-4704-1849-6)
• 160 A Course in Analytic Number Theory, Marius Overholt (2014, ISBN 978-1-4704-1706-2)
• 161 Introduction to Tropical Geometry, Diane Maclagan, Bernd Sturmfels (2015, ISBN 978-0-8218-5198-2)
• 162 A Course on Large Deviations with an Introduction to Gibbs Measures, Firas Rassoul-Agha, Timo Seppäläinen (2015, ISBN 978-0-8218-7578-0)
• 163 Introduction to Analytic and Probabilistic Number Theory, Gérald Tenenbaum (2015, 3rd ed., ISBN 978-0-8218-9854-3)
• 164 Expansion in Finite Simple Groups of Lie Type, Terence Tao (2015, ISBN 978-1-4704-2196-0)
• 165 Advanced Modern Algebra, Part 1, Joseph J. Rotman (2015, 3rd ed., ISBN 978-1-4704-1554-9)[13]
• 166 Problems in Real and Functional Analysis, Alberto Torchinsky (2015, ISBN 978-1-4704-2057-4)
• 167 Singular Perturbation in the Physical Sciences, John C. Neu (2015, ISBN 978-1-4704-2555-5)
• 168 Random Operators: Disorder Effects on Quantum Spectra and Dynamics, Michael Aizenman, Simone Warzel (2015, ISBN 978-1-4704-1913-4)
• 169 Partial Differential Equations: An Accessible Route through Theory and Applications, András Vasy (2015, ISBN 978-1-4704-1881-6)
• 170 Colored Operads, Donald Yau (2016, ISBN 978-1-4704-2723-8)
• 171 Nonlinear Elliptic Equations of the Second Order, Qing Han (2016, ISBN 978-1-4704-2607-1)
• 172 Combinatorics and Random Matrix Theory, Jinho Baik, Percy Deift, Toufic Suidan (2016, ISBN 978-0-8218-4841-8)
• 173 Differentiable Dynamical Systems: An Introduction to Structural Stability and Hyperbolicity, Lan Wen (2016, ISBN 978-1-4704-2799-3)
• 174 Quiver Representations and Quiver Varieties, Alexander Kirillov Jr. (2016, ISBN 978-1-4704-2307-0)
• 175 Cartan for Beginners: Differential Geometry via Moving Frames and Exterior Differential Systems, Thomas A. Ivey, Joseph M. Landsberg (2016, 2nd ed., ISBN 978-1-4704-0986-9)
• 176 Ordered Groups and Topology, Adam Clay, Dale Rolfsen (2016, ISBN 978-1-4704-3106-8)
• 177 Differential Galois Theory through Riemann-Hilbert Correspondence: An Elementary Introduction, Jacques Sauloy (2016, ISBN 978-1-4704-3095-5)
• 178 From Frenet to Cartan: The Method of Moving Frames, Jeanne N. Clelland (2017, ISBN 978-1-4704-2952-2)
• 179 Modular Forms: A Classical Approach, Henri Cohen, Fredrik Strömberg (2017, ISBN 978-0-8218-4947-7)
• 180 Advanced Modern Algebra, Part 2, Joseph J. Rotman (2017, 3rd ed., ISBN 978-1-4704-2311-7)[13]
• 181 A First Course in Sobolev Spaces, Giovanni Leoni (2017, 2nd ed., ISBN 978-1-4704-2921-8)
• 182 Nonlinear PDEs: A Dynamical Systems Approach, Guido Schneider, Hannes Uecker (2017, ISBN 978-1-4704-3613-1)
• 183 Separable Algebras, Timothy J. Ford (2017, ISBN 978-1-4704-3770-1)
• 184 An Introduction to Quiver Representations, Harm Derksen, Jerzy Weyman (2017, ISBN 978-1-4704-2556-2)
• 185 Braid Foliations in Low-Dimensional Topology, Douglas J. LaFountain, William W. Menasco (2017, ISBN 978-1-4704-3660-5)
• 186 Rational Points on Varieties, Bjorn Poonen (2017, ISBN 978-1-4704-3773-2)
• 187 Introduction to Global Analysis: Minimal Surfaces in Riemannian Manifolds, John Douglas Moore (2017, ISBN 978-1-4704-2950-8)
• 188 Introduction to Algebraic Geometry, Steven Dale Cutkosky (2018, ISBN 978-1-4704-3518-9)
• 189 Characters of Solvable Groups, I. Martin Isaacs (2018, ISBN 978-1-4704-3485-4)
• 190 Lectures on Finite Fields, Xiang-dong Hou (2018, ISBN 978-1-4704-4289-7)
• 191 Functional Analysis, Theo Bühler, Dietmar A. Salamon (2018, ISBN 978-1-4704-4190-6)
• 192 Lectures on Navier-Stokes Equations, Tai-Peng Tsai (2018, ISBN 978-1-4704-3096-2)
• 193 A Tour of Representation Theory, Martin Lorenz (2018, ISBN 978-1-4704-3680-3)
• 194 Algebraic Statistics, Seth Sullivant (2018, ISBN 978-1-4704-3517-2)
• 195 Combinatorial Reciprocity Theorems:An Invitation to Enumerative Geometric Combinatorics, Matthias Beck, Raman Sanyal (2018, ISBN 978-1-4704-2200-4)
• 196 Convection-Diffusion Problems:An Introduction to Their Analysis and Numerical Solution, Martin Stynes, David Stynes (2018, ISBN 978-1-4704-4868-4)
• 197 A Course on Partial Differential Equations, Walter Craig (2018, ISBN 978-1-4704-4292-7)
• 198 Dynamics in One Non-Archimedean Variable, Robert L Benedetto (2019, ISBN 978-1-4704-4688-8)
• 199 Applied Stochastic Analysis, Weinan E, Tiejun Li, Eric Vanden-Eijnden (2019, ISBN 978-1-4704-4933-9)
• 200 Mathematical Theory of Scattering Resonances, Semyon Dyatlov, Maciej Zworski (2019, ISBN 978-1-4704-4366-5)
• 201 Geometric Relativity, Dan A Lee (2019, ISBN 978-1-4704-5081-6)
• 202 Introduction to Complex Analysis, Michael E Taylor (2019, ISBN 978-1-4704-5286-5)
• 203 The Distribution of Prime Numbers, Dimitris Koukoulopoulos (2019, ISBN 978-1-4704-4754-0)
• 204 Hochschild Cohomology for Algebras, Sarah J. Witherspoon (2019, ISBN 978-1-4704-4931-5)
• 205 Invitation to Partial Differential Equations, Maxim Braverman, Robert McOwen, Peter Topalov, Mikhail Shubin (2020, ISBN 978-0-8218-3640-8)
• 206 Extrinsic Geometric Flows, Ben Andrews, Bennett Chow, Christine Guenther, Mat Langford (2020, ISBN 978-1-4704-5596-5)
• 207 Organized Collapse: An Introduction to Discrete Morse Theory, Dmitry N. Kozlov (2020, ISBN 978-1-4704-5701-3)
• 208 Geometry and Topology of Manifolds: Surfaces and Beyond, Vicente Muñoz, Ángel González-Prieto, Juan Ángel Rojo (2020, ISBN 978-1-4704-6132-4)
• 209 Hyperbolic Knot Theory, Jessica Purcell (2020, ISBN 978-1-4704-5499-9)
• 210 Combinatorics: The Art of Counting, Bruce E. Sagan (2020, ISBN 978-1-4704-6032-7)
• 211 Invitation to Nonlinear Algebra, Mateusz Michałek, Bernd Sturmfels (2021, ISBN 978-1-4704-6551-3)

---

Undergraduate Texts in Mathematics

List of books[edit]

1. Halmos, Paul R. (1974). Finite-Dimensional Vector Spaces. ISBN 978-0-387-90093-3.
2. Halmos, Paul Richard (1974). Lectures on Boolean algebras. ISBN 978-0-387-90094-0.
3. Halmos, Paul R. (1974). Naive Set Theory. ISBN 978-0-387-90092-6.
4. Martin, George E. (1975). The Foundations of Geometry and the Non-Euclidean Plane. ISBN 978-1-4612-5727-1.
5. Kemeny, John G.; Snell, J. Laurie (1976). Finite Markov Chains: With a New Appendix: “Generalization of a Fundamental Matrix”. ISBN 978-0-387-90192-3.
6. Singer, I. M.; Thorpe, J. A. (1976). Lecture Notes on Elementary Topology and Geometry. ISBN 978-0-387-90202-9.
7. Apostol, Tom M. (1976). Introduction to Analytic Number Theory. ISBN 978-0-387-90163-3.
8. Sigler, L. E. (1976). Algebra. ISBN 978-0-387-90195-4.
9. Fleming, Wendell (1977). Functions of Several Variables. ISBN 978-0-387-90206-7.
10. Croom, F. H. (1978). Basic Concepts of Algebraic Topology. ISBN 978-0-387-90288-3.
11. LeCuyer, Edward J. (1978). Introduction to College Mathematics with A Programming Language. ISBN 978-0-387-90280-7.
12. Duda, E.; Whyburn, G. (1979). Dynamic Topology. ISBN 978-0-387-90358-3.
13. Jantosciak, J.; Prenowitz, W. (1979). Join Geometries: A Theory of Convex Sets and Linear Geometry. ISBN 978-0-387-90340-8.
14. Malitz, Jerome (1979). Introduction to Mathematical Logic: Set Theory - Computable Functions - Model Theory. ISBN 978-0-387-90346-0.
15. Wilson, R. L. (1979). Much Ado About Calculus: A Modern Treatment with Applications Prepared for Use with the Computer. ISBN 978-0-387-90347-7.
16. Thorpe, John A. (1979). Elementary Topics in Differential Geometry. doi:10.1007/978-1-4612-6153-7. ISBN 978-0-387-90357-6.
17. Franklin, Joel (1980). Methods of Mathematical Economics: Linear and Nonlinear Programming. Fixed-Point Theorems. ISBN 978-0-387-90481-8.
18. Macki, Jack; Strauss, Aaron (1981). Introduction to Optimal Control Theory. ISBN 978-0-387-90624-9.
19. Foulds, L. R. (1981). Optimization Techniques: An Introduction. ISBN 978-0-387-90586-0.
20. Fischer, E. (1982). Intermediate Real Analysis. ISBN 978-0-387-90721-5.
21. Martin, George E. (1982). Transformation Geometry: An Introduction to Symmetry. ISBN 978-0-387-90636-2.
22. Martin, George E. (1983). The Foundations of Geometry and the Non-Euclidean Plane. ISBN 978-0-387-90694-2.
23. Owen, David R. (1983). A First Course in the Mathematical Foundations of Thermodynamics. ISBN 978-0-387-90897-7.
24. Smith, K. T. (1983). Primer of Modern Analysis: Directions for Knowing All Dark Things, Rhind Papyrus, 1800 B.C. ISBN 978-0-387-90797-0.
25. Armstrong, M. A. (1983). Basic Topology. doi:10.1007/978-1-4757-1793-8. ISBN 978-0-387-90839-7.
26. Dixmier, Jacques (1984). General Topology. ISBN 0-387-90972-9.
27. Morrey, Charles B. Jr.; Protter, Murray H. (1984). Intermediate Calculus. ISBN 978-0-387-96058-6.
28. Curtis, Charles W. (1984). Linear Algebra: An Introductory Approach. ISBN 978-0-387-90992-9.
29. Driver, R.D. (1984). Why Math?. ISBN 978-0-387-90973-8.
30. Foulds, L. R. (1984). Combinatorial Optimization for Undergraduates. ISBN 978-0-387-90977-6.
31. Jänich, Klaus (1984). Topology. ISBN 978-0-387-90892-2.
32. Bühler, W. K.; Cornell, G.; Opolka, H.; Scharlau, W. (1985). From Fermat to Minkowski: Lectures on the Theory of Numbers and Its Historical Development. ISBN 978-0-387-90942-4.
33. Marsden, Jerrold; Weinstein, Alan (1985). Calculus I. ISBN 978-0-387-90974-5.
34. Marsden, Jerrold; Weinstein, Alan (1985). Calculus II. ISBN 978-0-387-90975-2.
35. Marsden, Jerrold; Weinstein, Alan (1985). Calculus III. ISBN 978-0-387-90985-1.
36. Lang, Serge (1986). Introduction to Linear Algebra (2nd ed.). ISBN 978-0-387-96205-4.
37. Stanton, Dennis; White, Dennis (1986). Constructive Combinatorics. ISBN 978-0-387-96347-1.
38. Klambauer, Gabriel (1986). Aspects of Calculus. ISBN 978-0-387-96274-0.
39. Lang, Serge (1986). A First Course in Calculus (5th ed.). doi:10.1007/978-1-4419-8532-3. ISBN 978-0-387-96201-6.
40. James, I. M. (1987). Topological and Uniform Spaces. ISBN 978-0-387-96466-9.
41. Lang, Serge (1987). Calculus of Several Variables. ISBN 978-0-387-96405-8.
42. Lang, Serge (1987). Linear Algebra (3rd ed.). ISBN 978-0-387-96412-6.
43. Peressini, Anthony L.; Sullivan, Francis E.; Uhl, J.J. Jr. (1988). The Mathematics of Nonlinear Programming. ISBN 978-0-387-96614-4.
44. Samuel, Pierre (1988). Projective Geometry. ISBN 978-0-387-96752-3.
45. Armstrong, Mark A. (1988). Groups and Symmetry. doi:10.1007/978-1-4757-4034-9. ISBN 978-0-387-96675-5.
46. Brémaud, Pierre (1988). An Introduction to Probabilistic Modeling. doi:10.1007/978-1-4612-1046-7. ISBN 978-0-387-96460-7.
47. Bressoud, David M. (1989). Factorization and Primality Testing. doi:10.1007/978-1-4612-4544-5. ISBN 978-0-387-97040-0.
48. Brickman, Louis (1989). Mathematical Introduction to Linear Programming and Game Theory. doi:10.1007/978-1-4612-4540-7. ISBN 978-0-387-96931-2.
49. Strayer, James K. (1989). Linear Programming and Its Applications. doi:10.1007/978-1-4612-1009-2. ISBN 978-0-387-96930-5.
50. Flanigan, Francis J.; Kazdan, Jerry L. (1990). Calculus Two: Linear and Nonlinear Functions (2nd ed.). ISBN 978-0-387-97388-3.
51. Iooss, Gérard; Joseph, Daniel D. (1990). Elementary Stability and Bifurcation Theory (2nd ed.). doi:10.1007/978-1-4612-0997-3. ISBN 978-0-387-97068-4.
52. Hoffmann, Karl-Heinz; Hämmerlin, Günther (1991). Numerical Mathematics. doi:10.1007/978-1-4612-4442-4. ISBN 978-0-387-97494-1.
53. Morrey, Charles B. Jr.; Protter, Murray H. (1991). A First Course in Real Analysis (2nd ed.). doi:10.1007/978-1-4419-8744-0. ISBN 978-0-387-97437-8.
54. Bressoud, David M. (1991). Second Year Calculus: From Celestial Mechanics to Special Relativity. doi:10.1007/978-1-4612-0959-1. ISBN 978-0-387-97606-8.
55. Millman, Richard S.; Parker, George D. (1991). Geometry: A Metric Approach with Models (2nd ed.). ISBN 978-0-387-97412-5.
56. Palka, Bruce P. (1991). An Introduction to Complex Function Theory. ISBN 978-0-387-97427-9.
57. Banchoff, Thomas; Wermer, John (1992). Linear Algebra Through Geometry (2nd ed.). doi:10.1007/978-1-4612-4390-8. ISBN 978-0-387-97586-3.
58. Devlin, Keith (1993). The Joy of Sets: Fundamentals of Contemporary Set Theory (2nd ed.). doi:10.1007/978-1-4612-0903-4. ISBN 978-0-387-94094-6.
59. Kinsey, L. Christine (1993). Topology of Surfaces. doi:10.1007/978-1-4612-0899-0. ISBN 978-0-387-94102-8.
60. Valenza, Robert J. (1993). Linear Algebra: An Introduction to Abstract Mathematics. doi:10.1007/978-1-4612-0901-0. ISBN 978-0-387-94099-1.
61. Ebbinghaus, H. -D.; Flum, J.; Thomas, W. (1994). Mathematical Logic (2nd ed.). doi:10.1007/978-1-4757-2355-7. ISBN 978-0-387-94258-2.
62. Berberian, Sterling K. (1994). A First Course in Real Analysis. doi:10.1007/978-1-4419-8548-4. ISBN 978-0-387-94217-9.
63. Jänich, Klaus (1994). Linear Algebra. doi:10.1007/978-1-4612-4298-7. ISBN 978-0-387-94128-8.
64. Pedrick, George (1994). A First Course in Analysis. doi:10.1007/978-1-4419-8554-5. ISBN 978-0-387-94108-0.
65. Stillwell, John (1994). Elements of Algebra: Geometry, Numbers, Equations. doi:10.1007/978-1-4757-3976-3. ISBN 978-0-387-94290-2.
66. Anglin, W.S. (1994). Mathematics: A Concise History and Philosophy. doi:10.1007/978-1-4612-0875-4. ISBN 978-0-387-94280-3.
67. Simmonds, James G. (1994). A Brief on Tensor Analysis (2nd ed.). doi:10.1007/978-1-4419-8522-4. ISBN 978-0-387-94088-5.
68. Anglin, W.S.; Lambek, J. (1995). The Heritage of Thales. ISBN 978-0-387-94544-6.
69. Isaac, Richard (1995). The Pleasures of Probability. ISBN 978-0-387-94415-9.
70. Exner, George R. (1996). An Accompaniment to Higher Mathematics. doi:10.1007/978-1-4612-3998-7. ISBN 978-0-387-94617-7.
71. Troutman, John L. (1996). Variational Calculus and Optimal Control: Optimization with Elementary Convexity (2nd ed.). doi:10.1007/978-1-4612-0737-5. ISBN 978-0-387-94511-8.
72. Browder, Andrew (1996). Mathematical Analysis: An Introduction. doi:10.1007/978-1-4612-0715-3. ISBN 978-0-387-94614-6.
73. Buskes, Gerard; Rooij, Arnoud Van (1997). Topological Spaces: From Distance to Neighborhood. doi:10.1007/978-1-4612-0665-1. ISBN 978-0-387-94994-9.
74. Fine, Benjamin; Rosenberger, Gerhard (1997). The Fundamental Theorem of Algebra. doi:10.1007/978-1-4612-1928-6. ISBN 978-0-387-94657-3.
75. Beardon, Alan F. (1997). Limits: A New Approach to Real Analysis. doi:10.1007/978-1-4612-0697-2. ISBN 978-0-387-98274-8.
76. Gordon, Hugh (1997). Discrete Probability. doi:10.1007/978-1-4612-1966-8. ISBN 978-0-387-98227-4.
77. Roman, Steven (1997). Introduction to Coding and Information Theory. ISBN 978-0-387-94704-4.
78. Sethuraman, Bharath (1997). Rings, Fields, and Vector Spaces: An Introduction to Abstract Algebra via Geometric Constructibility. doi:10.1007/978-1-4757-2700-5. ISBN 978-0-387-94848-5.
79. Lang, Serge (1997). Undergraduate Analysis (2nd ed.). doi:10.1007/978-1-4757-2698-5. ISBN 978-0-387-94841-6.
80. Hilton, Peter; Holton, Derek; Pedersen, Jean (1997). Mathematical Reflections: In a Room with Many Mirrors. doi:10.1007/978-1-4612-1932-3. ISBN 978-0-387-94770-9.
81. Martin, George E. (1998). Geometric Constructions. doi:10.1007/978-1-4612-0629-3. ISBN 978-0-387-98276-2.
82. Protter, Murray H. (1998). Basic Elements of Real Analysis. doi:10.1007/b98884. ISBN 978-0-387-98479-7.
83. Priestley, W. M. (1998). Calculus: A Liberal Art (2nd ed.). doi:10.1007/978-1-4612-1658-2. ISBN 978-0-387-98379-0.
84. Singer, David A. (1998). Geometry: Plane and Fancy. doi:10.1007/978-1-4612-0607-1. ISBN 978-0-387-98306-6.
85. Smith, Larry (1998). Linear Algebra (3rd ed.). doi:10.1007/978-1-4612-1670-4. ISBN 978-0-387-98455-1.
86. Lidl, Rudolf; Pilz, Günter (1998). Applied Abstract Algebra (2nd ed.). doi:10.1007/978-1-4757-2941-2. ISBN 978-0-387-98290-8.
87. Stillwell, John (1998). Numbers and Geometry. doi:10.1007/978-1-4612-0687-3. ISBN 978-0-387-98289-2.
88. Laubenbacher, Reinhard; Pengelley, David (1999). Mathematical Expeditions: Chronicles by the Explorers. ISBN 978-0-387-98434-6.
89. Frazier, Michael W. (1999). An Introduction to Wavelets Through Linear Algebra. ISBN 978-0-387-98639-5.
90. Schiff, Joel L. (1999). The Laplace Transform: Theory and Applications. ISBN 978-0-387-98698-2.
91. Brunt, B. van; Carter, M. (2000). The Lebesgue-Stieltjes Integral: A Practical Introduction. doi:10.1007/978-1-4612-1174-7. ISBN 978-0-387-95012-9.
92. Exner, George R. (2000). Inside Calculus. doi:10.1007/b97700. ISBN 978-0-387-98932-7.
93. Hartshorne, Robin (2000). Geometry: Euclid and Beyond. doi:10.1007/978-0-387-22676-7. ISBN 978-0-387-98650-0.
94. Callahan, James J. (2000). The Geometry of Spacetime: An Introduction to Special and General Relativity. doi:10.1007/978-1-4757-6736-0. ISBN 978-0-387-98641-8.
95. Cederberg, Judith N. (2001). A Course in Modern Geometries (2nd ed.). doi:10.1007/978-1-4757-3490-4. ISBN 978-0-387-98972-3.
96. Gamelin, Theodore W. (2001). Complex Analysis. doi:10.1007/978-0-387-21607-2. ISBN 978-0-387-95093-8.
97. Jänich, Klaus (2001). Vector Analysis. doi:10.1007/978-1-4757-3478-2. ISBN 978-0-387-98649-4.
98. Martin, George E. (2001). Counting: The Art of Enumerative Combinatorics. doi:10.1007/978-1-4757-4878-9. ISBN 978-0-387-95225-3.
99. Hilton, Peter; Holton, Derek; Pedersen, Jean (2002). Mathematical Vistas: From a Room with Many Windows. doi:10.1007/978-1-4757-3681-6. ISBN 978-0-387-95064-8.
100. Saxe, Karen (2002). Beginning Functional Analysis. doi:10.1007/978-1-4757-3687-8. ISBN 978-0-387-95224-6.
101. Lang, Serge (2002). Short Calculus: The Original Edition of “A First Course in Calculus”. doi:10.1007/978-1-4613-0077-9. ISBN 978-0-387-95327-4.
102. Estep, Donald (2002). Practical Analysis in One Variable. doi:10.1007/b97698. ISBN 978-0-387-95484-4.
103. Toth, Gabor (2002). Glimpses of Algebra and Geometry (2nd ed.). doi:10.1007/b98964. ISBN 978-0-387-95345-8.
104. Aitsahlia, Farid; Chung, Kai Lai (2003). Elementary Probability Theory: With Stochastic Processes and an Introduction to Mathematical Finance (4th ed.). doi:10.1007/978-0-387-21548-8. ISBN 978-0-387-95578-0.
105. Erdös, Paul; Suranyi, Janos (2003). Topics in the Theory of Numbers. doi:10.1007/978-1-4613-0015-1. ISBN 978-0-387-95320-5.
106. Lovász, L.; Pelikán, J.; Vesztergombi, K. (2003). Discrete Mathematics: Elementary and Beyond. doi:10.1007/b97469. ISBN 978-0-387-95584-1.
107. Stillwell, John (2003). Elements of Number Theory. doi:10.1007/978-0-387-21735-2. ISBN 978-0-387-95587-2.
108. Buchmann, Johannes (2004). Introduction to Cryptography (2nd ed.). doi:10.1007/978-1-4419-9003-7. ISBN 978-0-387-21156-5.
109. Irving, Ronald S. (2004). Integers, Polynomials, and Rings: A Course in Algebra. doi:10.1007/b97633. ISBN 978-0-387-40397-7.
110. Ross, Clay C. (2004). Differential Equations: An Introduction with Mathematica (2nd ed.). doi:10.1007/978-1-4757-3949-7. ISBN 978-0-387-21284-5.
111. Cull, Paul; Flahive, Mary; Robson, Robby (2005). Difference Equations: From Rabbits to Chaos. doi:10.1007/0-387-27645-9. ISBN 978-0-387-23233-1.
112. Chambert-Loir, Antoine (2005). A Field Guide to Algebra. doi:10.1007/b138364. ISBN 978-0-387-21428-3.
113. Elaydi, Saber (2005). An Introduction to Difference Equations (3rd ed.). doi:10.1007/0-387-27602-5. ISBN 978-0-387-23059-7.
114. Lang, Serge (2005). Undergraduate Algebra (3rd ed.). doi:10.1007/0-387-27475-8. ISBN 978-0-387-22025-3.
115. Singer, Stephanie Frank (2005). Linearity, Symmetry, and Prediction in the Hydrogen Atom. doi:10.1007/b136359. ISBN 978-0-387-24637-6.
116. Stillwell, John (2005). The Four Pillars of Geometry. doi:10.1007/0-387-29052-4. ISBN 978-0-387-25530-9.
117. Bix, Robert (2006). Conics and Cubics: A Concrete Introduction to Algebraic Curves (2nd ed.). doi:10.1007/0-387-39273-4. ISBN 978-0-387-31802-8.
118. Moschovakis, Yiannis (2006). Notes on Set Theory (2nd ed.). doi:10.1007/0-387-31609-4. ISBN 978-0387287225.
119. Knoebel, Art; Laubenbacher, Reinhard; Lodder, Jerry; Pengelley, David (2007). Mathematical Masterpieces: Further Chronicles by the Explorers. doi:10.1007/978-0-387-33062-4. ISBN 978-0-387-33060-0.
120. Harris, John M.; Hirst, Jeffry L.; Mossinghoff, Michael (2008). Combinatorics and Graph Theory (2nd ed.). doi:10.1007/978-0-387-79711-3. ISBN 978-0-387-79710-6.
121. Stillwell, John (2008). Naive Lie Theory. doi:10.1007/978-0-387-78214-0. ISBN 978-0-387-78214-0.
122. Hairer, Ernst; Wanner, Gerhard (2008) [1996]. Analysis by its History. doi:10.1007/978-0-387-77036-9. ISBN 978-0-387-94551-4.
123. Edgar, Gerald (2008). Edgar, Gerald (ed.). Measure, Topology, and Fractal Geometry (2nd ed.). doi:10.1007/978-0-387-74749-1. ISBN 978-0-387-74748-4.
124. Herod, James; Shonkwiler, Ronald W. (2009). Mathematical Biology: An Introduction with Maple and Matlab (2nd ed.). doi:10.1007/978-0-387-70984-0. ISBN 978-0-387-70983-3.
125. Mendivil, Frank; Shonkwiler, Ronald W. (2009). Explorations in Monte Carlo Methods. doi:10.1007/978-0-387-87837-9. ISBN 978-0-387-87836-2.
126. Stein, William (2009). Elementary Number Theory: Primes, Congruences, and Secrets: A Computational Approach. doi:10.1007/b13279. ISBN 978-0-387-85524-0.
127. Childs, Lindsay N. (2009). Childs, Lindsay N (ed.). A Concrete Introduction to Higher Algebra (3rd ed.). doi:10.1007/978-0-387-74725-5. ISBN 978-0-387-74527-5.
128. Halmos, Paul R.; Givant, Steven (2009). Introduction to Boolean Algebras. doi:10.1007/978-0-387-68436-9. ISBN 978-0-387-40293-2.
129. Bak, Joseph; Newman, Donald J. (2010). Complex Analysis (3rd ed.). doi:10.1007/978-1-4419-7288-0. ISBN 978-1-4419-7287-3.
130. Beck, Matthias; Geoghegan, Ross (2010). The Art of Proof: Basic Training for Deeper Mathematics. doi:10.1007/978-1-4419-7023-7. ISBN 978-1-4419-7022-0.
131. Callahan, James J. (2010). Advanced Calculus: A Geometric View. ISBN 978-1-4419-7331-3.
132. Hurlbert, Glenn (2010). Linear Optimization: The Simplex Workbook. ISBN 978-0-387-79147-0.
133. Stillwell, John (2010). Mathematics and Its History (3rd ed.). doi:10.1007/978-1-4419-6053-5. ISBN 978-1-441-96052-8.
134. Ghorpade, Sudhir R.; Limaye, Balmohan V. (2010). A Course in Multivariable Calculus and Analysis. doi:10.1007/978-1-4419-1621-1. ISBN 978-1-4419-1620-4.
135. Davidson, Kenneth R.; Donsig, Allan P. (2010). Real Analysis and Applications: Theory in Practice. doi:10.1007/978-0-387-98098-0. ISBN 978-0-387-98097-3.
136. Daepp, Ulrich; Gorkin, Pamela (2011). Reading, Writing, and Proving: A Closer Look at Mathematics (2nd ed.). doi:10.1007/978-1-4419-9479-0. ISBN 978-1-4419-9478-3.
137. Bloch, Ethan D. (2011). Proofs and Fundamentals: A First Course in Abstract Mathematics (2nd ed.). doi:10.1007/978-1-4419-7127-2. ISBN 978-1-4419-7126-5.
138. Adkins, William A.; Davidson, Mark G. (2012). Ordinary Differential Equations. ISBN 978-1-461-43617-1.
139. Ostermann, Alexander; Wanner, Gerhard (2012). Geometry by Its History. ISBN 978-3-642-29163-0.
140. Petersen, Peter (2012). Linear Algebra. ISBN 978-1-4614-3612-6.
141. Roman, Steven (2012). Introduction to the Mathematics of Finance: Arbitrage and Option Pricing. ISBN 978-1-4614-3582-2.
142. Gerstein, Larry J. (2012). Introduction to Mathematical Structures and Proofs (2nd ed.). doi:10.1007/978-1-4614-4265-3. ISBN 978-1-4614-4264-6.
143. Vanderbei, Robert J.; Çinlar, Erhan (2013). Real and Convex Analysis. ISBN 978-1-4614-5256-0.
144. Bajnok, Bela (2013). An Invitation to Abstract Mathematics. ISBN 978-1-461-46635-2.
145. McInerney, Andrew (2013). First Steps in Differential Geometry. ISBN 978-1-4614-7731-0.
146. Ross, Kenneth A. (2013). Elementary Analysis: The Theory of Calculus. ISBN 978-1-4614-6270-5.
147. Stillwell, John (2013). The Real Numbers: An Introduction to Set Theory and Analysis. doi:10.1007/978-3-319-01577-4. ISBN 978-3-319-01576-7.
148. Conway, John B. (2014). A Course in Point Set Topology. ISBN 978-3-319-02367-0.
149. Olver, Peter J. (2014). Introduction to Partial Differential Equations. ISBN 978-3-319-02098-3.
150. Mercer, Peter R. (2014). More Calculus of a Single Variable. doi:10.1007/978-1-4939-1926-0. ISBN 978-1-4939-1925-3.
151. Hoffstein, Jeffrey; Pipher, Jill; Silverman, Joseph H. (2014). An Introduction to Mathematical Cryptography (2nd ed.). doi:10.1007/978-1-4939-1711-2. ISBN 978-1-4939-1710-5.
152. Terrell, Maria Shea; Lax, Peter D. (2014). Calculus with Applications (2nd ed.). doi:10.1007/978-1-4614-7946-8. ISBN 978-1-4614-7945-1.
153. Axler, Sheldon (2015). Linear Algebra Done Right (3rd ed.). doi:10.1007/978-3-319-11080-6. ISBN 978-3-319-11079-0.
154. Beck, Matthias; Robins, Sinai (2015). Computing the Continuous Discretely: Integer-point Enumeration in Polyhedra (2nd ed.). doi:10.1007/978-1-4939-2969-6. ISBN 978-1-4939-2968-9.
155. Laczkovich, Miklós; Sós, Vera T. (2015). Real Analysis: Foundations and Functions of One Variable. doi:10.1007/978-1-4939-2766-1. ISBN 978-1-4939-2765-4.
156. Pugh, Charles C. (2015). Real Mathematical Analysis (2nd ed.). doi:10.1007/978-3-319-17771-7. ISBN 978-3-319-17770-0.
157. Logan, David J. (2015). A First Course in Differential Equations (3rd ed.). doi:10.1007/978-3-319-17852-3. ISBN 978-3-319-17851-6.
158. Silverman, Joseph H.; Tate, John (2015). Rational Points on Elliptic Curves (2nd ed.). doi:10.1007/978-3-319-18588-0. ISBN 978-3-319-18587-3.
159. Little, Charles; Kee, Teo; van Brunt, Bruce (2015). Real Analysis via Sequences and Series. doi:10.1007/978-1-4939-2651-0. ISBN 978-1-4939-2650-3.
160. Abbott, Stephen (2015). Understanding Analysis (2nd ed.). doi:10.1007/978-1-4939-2712-8. ISBN 978-1-4939-2711-1.
161. Cox, David; Little, John; O’Shea, Danal (2015). Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra (4th ed.). doi:10.1007/978-3-319-16721-3. ISBN 978-3-319-16720-6.
162. Logan, David J. (2015). Applied Partial Differential Equations (3rd ed.). doi:10.1007/978-3-319-12493-3. ISBN 978-3-319-12492-6.
163. Tapp, Kristopher (2016). Differential Geometry of Curves and Surfaces. doi:10.1007/978-3-319-39799-3. ISBN 978-3-319-39798-6.
164. Hijab, Omar (2016). Introduction to Calculus and Classical Analysis (4th ed.). doi:10.1007/978-3-319-28400-2. ISBN 978-3-319-28399-9.
165. Shurman, Jerry (2016). Calculus and Analysis in Euclidean Space. doi:10.1007/978-3-319-49314-5. ISBN 978-3-319-49312-1.
166. Laczkovich, Miklós; Sós, Vera T. (2017). Real Analysis: Series, Functions of Several Variables, and Applications. doi:10.1007/978-1-4939-7369-9. ISBN 978-1-4939-7367-5.
167. Lax, Peter D.; Terrell, Maria Shea (2017). Multivariable Calculus with Applications. doi:10.1007/978-3-319-74073-7. ISBN 978-3-319-74072-0.
168. Shores, Thomas S. (2018). Applied Linear Algebra and Matrix Analysis (2nd ed.). doi:10.1007/978-3-319-74748-4. ISBN 978-3-319-74747-7.
169. Olver, Peter J.; Shakiban, Chehrzad (2018). Applied Linear Algebra (2nd ed.). doi:10.1007/978-3-319-91041-3. ISBN 978-3-319-91040-6.
170. Stanley, Richard P. (2018). Algebraic Combinatorics: Walks, Trees, Tableaux, and More (2nd ed.). doi:10.1007/978-3-319-77173-1. ISBN 978-3-319-77172-4.
171. Ghorpade, Sudhir R.; Limaye, Balmohan V. (2018). A Course in Calculus and Real Analysis (2nd ed.). doi:10.1007/978-3-030-01400-1. ISBN 978-3-030-01399-8.
172. Asmar, Nakhle H.; Grafakos, Loukas (2018). Complex Analysis with Applications. doi:10.1007/978-3-319-94063-2. ISBN 978-3-319-94062-5.
173. Rosenthal, Daniel; Rosenthal, David; Rosenthal, Peter (2018). A Readable Introduction to Real Mathematics (2nd ed.). doi:10.1007/978-3-030-00632-7. ISBN 978-3-030-00631-0.
174. Takloo-Bighash, Ramin (2018). A Pythagorean Introduction to Number Theory. doi:10.1007/978-3-030-02604-2. ISBN 978-3-030-02603-5.
175. Petersen, T. Kyle (2019). Inquiry-Based Enumerative Combinatorics: One, Two, Skip a Few… Ninety-Nine, One Hundred. doi:10.1007/978-3-030-18308-0. ISBN 978-3-030-18307-3.
176. Saari, Donald G. (2019). Mathematics of Finance: An Intuitive Introduction. doi:10.1007/978-3-030-25443-8. ISBN 978-3-030-25442-1.
177. Jongsma, Calvin (2019). Introduction to Discrete Mathematics via Logic and Proof. doi:10.1007/978-3-030-25358-5. ISBN 978-3-030-25357-8.
178. Lee, Nam-Hoon (2020). Geometry: from Isometries to Special Relativity. doi:10.1007/978-3-030-42101-4. ISBN 978-3-030-42100-7.
179. Bajnok, Bela (2020). An Invitation to Abstract Mathematics (2nd ed.). doi:10.1007/978-3-030-56174-1. ISBN 978-3-030-56173-4.
180. Stillwell, John (2020). Mathematics and Its History. doi:10.1007/978-3-030-55193-3. ISBN 978-3-030-55192-6.

https://en.wikipedia.org/

---

制书科普

2016.06.18 更新@猫立刻 的指正，补充两个物理化学中的公式排版。

============================================================

（一）
国内，像高教出版社，化学工业出版社等，教材都是方正系统排的，使用的是方正的英文和数学字体。除非你自己有一套 D 版的方正排版系统，想排出和国内教材一模一样的效果，基本没有可能。

个人觉得国内教材上方正数学字体太细。你觉得国内教材书上的字体更好看，一定程度上有先入为主的因素，看习惯了某些样式，以为这些样式就是标准，就是美。自从我接触了 LaTeX 世界很多曲线饱满、优美的数学字体后，觉得方正的那套数学字体也是一般般。

（二）
即使你掌握了好的排版公式的软件或语言，也未必能排出工整像样的公式。比如，你有注意过理工科中的单位都是和数值间隔一小段间距吗？你有注意过，一般物理量用 Italic（所谓的「斜体」），而单位使用 Upright （正体）吗？比如

\documentclass{article}
\usepackage{siunitx}
\begin{document}
\[
    p = \SI{760}{\mmHg}
\]
not
\[
    \mathrm{p}=760\textit{mmHg}
\]
\end{document}

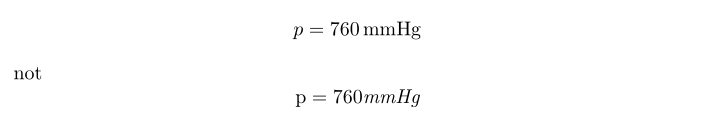
你有注意过很多国内教材，数学常数 π，e，虚数单位 i 都是使用正体；而像数学函数名，如正弦函数（sin），对数函数（log），一些算符，如导数的莱布尼兹符号（d，或者称作你们熟悉的「微分算符」），都是使用正体，而不是 Italic：

\documentclass{article}
\usepackage{amsmath}
\usepackage{upgreek}
\begin{document}
\noindent Either
\begin{equation}
	f(x) = \dfrac{1}{2\uppi}\int ^{\infty}_{-\infty}\hat{F}(k)\mathrm{e}^{\mathrm{i}kx}\mathrm{d}k \tag{ISO style}
\end{equation}
or
\begin{equation}
	f(x) = \dfrac{1}{2\pi}\int ^{\infty}_{-\infty}\hat{F}(k)e^{ikx}dk \tag{Conventional style}
\end{equation}
\end{document}

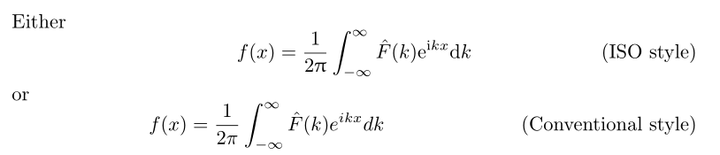
类似这样，对于数学物理公式和单位的排版原则，国内的正规出版教材的出版社，都是根据 国家标准《GB 3102.11-93 物理科学和技术中使用的数学符号》，这是一个对 ISO 31-11 和 ISO 80000-2:2009 标准的推广【1】：http://www.jgjs.net.cn/UserFiles/File/GB%203102.11-93.pdf

注意这个标准号是「GB」，不是「GB/T」，因此在中国大陆，这是一个强制标准。国外教材倒是没有这方面的限制（没有说一定要让圆周率 π，导数的莱布尼兹符号 d 以正体出现在出版物上，但是 sin，ln，log 这些函数名，为了和变量、物理量区分开，都是用 upright 形式）。

此外，某些人排公式，实在是对于美观不是很留心，比如，如果你让人蛋疼地排出了如下这个公式：

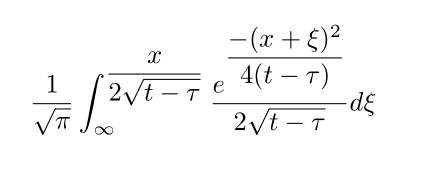
稍微注意一下，教材都是如何让复杂分式看起来不那么臃肿：

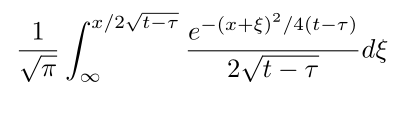
（三）

word 内置的数学公式排版功能，是使用微软自己的 Cambria Math 字体。这类字体，是基于 OpenType 数学扩展的特殊字体（普通的 OpenType 字体是不能随便用于排版数学公式），公式里的分式，根式，上下标，基线等等是由复杂的参数控制的，具体来说，是基于「数学排版参数表」（The mathematical typesetting table, 缩写是 MATH）【2】：MATH - The mathematical typesetting table

MATH 参数表是专门为 OpenType 字体设置公式中参数的表，这些参数受到 LaTeX 的数学公式参数的启发，并继承铅印时代排版数学公式的复杂结构：

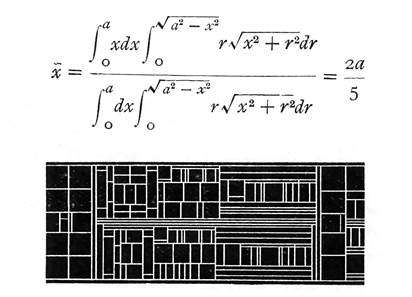
由微软公司开发完成，微软公式基于此参数表，开发出了第一款带有数学公式扩展的 OpenType 字体：Cambria Math，配合衬线字体 Cambria。

如果你不喜欢 Cambria Math，可以更换其它开源的、带有数学扩展支持的 OpenType 字体，只要下载这些字体的文件，复制粘贴到控制面板——字体里，你就能在 word 中使用：Fonts for Mozilla’s MathML engine

具体如何在 word 中将 数学模式下的 Cambria Math 更换成别的数学字体，请参见：http://jingyan.baidu.com/article/0f5fb0991cff3d6d8334ea33.html

注意，很多学校要求毕业论文的正文字体是 Times New Roman。这是 Monotype 公司设计的一款 TrueType 字体，虽然字母覆盖对于普通理工科学生是够用了，有扩展拉丁和希腊字母，也支持一部分特殊符号。但是没有配套的数学字体参数支持，不能用于排版数学公式（你用黑客技术，自己为 word 写插件，硬排也是有办法的，但不可避免会难看），而且众多用于数学公式，物理单位的 unicode 符号，Times New Roman 也没有为这些 glyph 设计相应的字体形状，你用 Times New Roman 是打不出那些符号的。一个比较好的替代方案，是使用开源的、支持 MATH 参数表的 Times 风格字体来代替（比如 TeX Gyre Termes，STIX 或 XITS 的 OpenType 字体，三款都是 Times 风格）。可以在 word 中使用。

（四）

（以下是更多关于数学字体和公式排版的信息，属于跑题内容……）

Springer 的很多教科书，基本上都是和 TeX 世界有关的排版做成的，国外很多理工教材都是扑面而来的 Computer Modern 系列字体（源于 TeX 世界，高德纳教授开发），有些国外的学术出版机构是使用商业数学字体，如 MathTime Professional（Times 风格，两个版本都是 Type 1 字体）。

现如今，绝大部分数学公式排版软件，功能，或多或少都受到了 TeX 的影响，或者是基于 TeX 对于数学公式参数的处理。TeX 是斯坦福大学高德纳教授（计算机科学家，Professor Donald Knuth）在上世纪 80 年代开发的一个排版系统，因为他无法忍受每况愈下的出版社排版，影响他出书，于是决定暂停他的出书计划，开发一个排版系统，采用先进的算法来实现断行，分页，间距，交叉引用，数学公式，文献目录等众多学术排版功能。由于 TeX 的语句对于普通用户来说过于复杂，美国的 Leslie Lamport 博士基于 TeX 开发出了 LaTeX 系统，现在大部分 TeX 用户，都是使用 LaTeX 的。

LaTeX 是排版数学公式是当之无愧的第一，也是出版界的事实标准。微软做 MATH 参数表，很多也是直接采用 TeX 对于公式处理的参数（微软为 LaTeX 做出了巨大的贡献，MATH 参数表的完成，使得在 LaTeX 中使用带有数学支持的 OpenType 字体成为了可能）。

主观一点，个人认为，很抱歉，我实在是认为，MathType 是垃圾……（非常抱歉，如果冒犯了忠实用户和开发者），是一个公式排版非常低端的实现，而且还收费。当然，工具没有绝对的高端低级，只要能让你觉得效率高，输出效果令你，你导师或者审查人满意，那么适合的才是最好的。

-————————————-

某些人认为我大 LaTeX 敲公式效率低，呵呵，一是你不熟悉 amsmath 的命令，二是你不会配置好的编辑器，插件，快捷键以及自动补全。等过了陡峭的学习曲线段，纯键盘操作，双手不离开键盘，绝对比你一会儿点鼠标，一会儿敲键盘，一会儿上网搜公式怎么敲快多了。至于这个学习成本是不是值得你付出，仁者见仁，智者见智，看情况。自从入了 GNU 世界的大坑，习惯文本文件，文本编辑器，git 版本管理，Emacs + org mode 记笔记，数据可视化和示意图都用矢量图格式……对于 word 这类单纯以二进制文件打开、保存我大段学术论文的东西，且对 Office 之外矢量图格式糟糕的支持，恕我实在是不太满意，也不放心……

2016.06.18 更新@猫立刻 的指正：另外.docx就是压缩的xml文件，不是那种“纯”二进制文件。很多人用Word是因为合作者只会Word。

-————————————–
看到答案中有人用 MathType 鼠标一键点出了物理化学中的两个频繁使用的公式。首先吐槽一下高教出版社的南京大学《物理化学》教材的排版（别误会我，这是我认为国内最好的物化教材，这个只是吹毛求疵的一个排版小槽点），目前的第五版中，依然没能排出一个很简单的「标准状态」符号，只能使用电学中的一个二元运算符（⊖，U+2296，TeX 中的命令通常是 \ominus）来代替，国外的教材，排不出这个符号的，也只能使用 ° 来代替。

TeX 世界中的创造力，也能体现在自己定义符号上，这里采用 Donald Arseneau 定义「标准状态」的方法，经由 Joseph Wright 在他的 chemstyle 宏包中改进，可以有如下效果

\documentclass{article}
\makeatletter
\providecommand*\stst{%
  {%
    \ensuremath{\protect\cst@stst}%
  }%
}
\newcommand*\cst@stst{%
  \mathpalette\cst@stst@aux\circ
}
\newcommand*\cst@stst@aux[2]{%
  \ooalign{%
    \hfil
    $#1-$%
    \hfil
    \cr
    \hfil
    $#1#2$%
    \hfil
    \cr
  }%
}
\makeatother

\begin{document}
\[
	\Delta _rG^{\stst}_m = \Delta _rH^{\stst}_m - T\Delta _rS^{\stst}_m 
\]
\end{document}

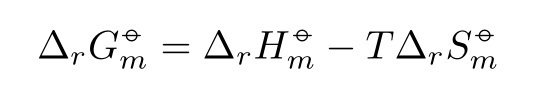
这标态符号的效果目前是要好于 MathType 吧？等 MathType 升级后，也许符号会变得更好看……

进一步吹毛求疵，觉得 r （reversible，可逆）和 m （molar，摩尔生成 XXX）应该用正体？好吧：

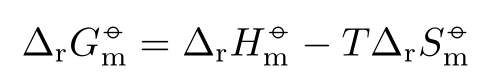
上下标的字体用 amsmath 宏包去调吧，调到满意为止。

==================================

参考资料

【1】李阿玲﹒《LaTeX 与 MathJax：数学公式与 web 呈现》﹒「学术与 TeX」微信公众号
【2】刘海洋﹒《LaTeX 入门》﹒电子科技出版社

---

https://tex.stackexchange.com/questions/47964/how-to-write-a-book-in-latex

---

AMS

Book Author Resources

The AMS values your contribution as an author and strives to provide you with all the information you need to help make your publication a success. The AMS Book Program concentrates on high-quality expository works, texts, and traditional research publications. By publishing with the AMS, your book will be part of one of the most respectable collections of mathematical literature in the world.

AMS Book Production Steps

Initial Submission | Produce Your Book | Submit Your Book | Post-Publication Information

Produce Your Book

Information for preparation of accepted books and articles

Complete information about the preparation of manuscripts for monographs and articles for proceedings volumes is available from the AMS. Authors of articles for conference proceedings normally receive this information automatically. If you have not received any such information, please contact the [Acquisitions Department](mailto:acquisitions@ams.org?Subject=Template for Page Layout for AMS Books).

Book Packages

The AMS Author and Editor Packages were designed to be used within an existing TeX system. You must have the following installed:

• TeX (available as freeware or shareware, or from commercial TeX vendors)
• LaTeX (including AMS-LaTeX extensions
• AMSFonts (if using extra symbols)

The AMS strongly encourages you to prepare your article using the appropriate LaTeX author package. You may retrieve a book package for any of the following types of publications:

• AMS Monographs:

  ​ Select from list CBMS Regional Conference Series in Mathematics (Monograph) Clay Mathematics Monographs Colloquium Publications CRM Monograph Series Graduate Studies in Mathematics History of Mathematics Mathematical Surveys and Monographs Mathematical World MSRI Mathematical Circles Library Pure and Applied Undergraduate Texts SMF/AMS Texts and Monographs Student Mathematical Library Translations of Mathematical Monographs Translations of Mathematical Monographs – Iwanami Series in Modern Mathematics University Lecture Series Generic Packages Generic Monograph

• AMS Collections & Proceedings volumes:

  ​ Select from list CBMS Issues in Mathematics Education (Proceedings) Clay Mathematics Proceedings Contemporary Mathematics (Proceedings) CRM Proceedings & Lecture Notes IAS/Park City Mathematics Series Proceedings of Symposia in Applied Mathematics Proceedings of Symposia in Pure Mathematics Translations – Series 2 Generic Packages Generic Proceedings or Collection

• MAA Monographs:

  ​ Select from list Anneli Lax New Mathematical Library Carus Mathematical Monographs Classroom Resource Materials Dolciani Mathematical Expositions AMS/MAA Textbooks Problem Books Spectrum

Each .zip file contains:

• a README file which should be read first
• an Author Handbook (available separately as a PDF file)
• guidelines for creating graphics (available separately as a PDF file)
• style files
• topmatter templates
• samples
• supplementary instructions

Need help with the .zip file?

AMS Author Handbook

Designed to help you prepare your book or article for publication or copublication by the AMS; contains information about all facets of the AMS publication process.

Graphics Guidelines

The Graphics Guidelines provide detailed instructions for creating and preparing graphics for inclusion in a book or article. Following these guidelines will help your projects move quickly through production.

Color Policy

• Monographs When a monograph includes color graphics, figures should have a resolution of at least 300 pixels per inch when printed at 100%. Ideally, they should be in EPS format; TIFF and JPEG are also acceptable. Note that PostScript is not the same as Encapsulated PostScript; the latter is a subset of the former.
• Collections and Proceedings The AMS normally does not include color graphics in its proceedings and collection volumes, except in special circumstances. When the Managing Editor and Publisher mutually agree that color graphics are warranted, figures should have a resolution of at least 300 pixels per inch when printed at 100%. Ideally, they should be in EPS format; TIFF and JPEG are also acceptable. Note that PostScript is not the same as Encapsulated PostScript; the latter is a subset of the former.

Consent to Publish and Copyright Agreement

After an article is accepted for publication, the AMS will send out a Consent to Publish Form to all authors of the article. All authors submitting papers to any proceedings volume must give the AMS specific permission to publish the work (“consent to publish”) by returning a signed consent form.

Permissions

• Permission to Use AMS Material: To use material published by the AMS, please [contact us](http://www.ams.org/cgi-bin/fmail/fmail.cgi?emailto=52616e646f6d49563ecb1a7ed316070f89a9b434ab38a68f4a4ad92e3ec175f878ea19b5b9c47a2bfb6c3b1aa0483a9b&name=Copyright & Permissions).
• Permission to Use Non-AMS Material: You must obtain written permission for the use of material, including text, graphics, photos, tables, and other art, that comes from any other source. As soon as your manuscript is accepted for publication, request permissions using the AMS permission form. Send a copy of the letter(s) granting permission to the AMS with your submission.

Technical Support

For expert advice and answers to questions about preparing or submitting your electronic submission after it has been accepted for publication, please contact the AMS Technical Support staff.

---

The Birth of a Physics Textbook: An Author’s Journey

Source https://www.physicsforums.com/insights/the-birth-of-a-textbook/

It is said that you should accomplish three things in life:

1. Plant a tree.
2. Have a child.
3. Write a book.

Out of the three, I have completed at least one. At the time of writing this Insight, my textbook “Mathematical Methods for Physics and Engineering” just hit the virtual online shelves. This Insight will describe the process leading to its creation, from the first seeds of an idea to where we are today. Although each textbook has its own story, I hope this one can satisfy the curiosity of anyone who wonders how some textbooks come to be.

The search for a textbook

As many of those who frequent the Physics Forums homework sections are aware, I am a university lecturer working in a theoretical physics department. When I started my tenure track position five years ago at my alma mater, I took over one of the courses I appreciated the most as a student and faced a conundrum that many educators will face when giving a course for the first time: Which textbook should I use? In this context, it should be mentioned that (unfortunately) students in the program I was teaching generally expect the course to be defined by the textbook and rarely acquire or consult textbook sources apart from the main coursebook. The choice of the textbook was therefore crucial.

The course covered four main topics: modeling physical systems using partial differential equations (PDEs), solving PDEs using orthogonal sets of functions, Green’s functions, and variational calculus. The course had been using a textbook in Swedish for some time, but it did not really cover variational calculus in a satisfactory manner and so I set out to search for an alternative. Among the books, I looked at were classics such as the books by Arfken et al, Boas, and Riley et al, but none of the books I found really satisfied the needs of the course. While some covered the necessary material, they often covered more material than necessary, did not cover some of the required topics in sufficient depth, or presented a majority of its examples using physics that my students were not yet familiar with (mainly quantum mechanics).

Due to its extensive coverage of topics, I ended up trying out Arfken as the main textbook the second time I gave the course. However, I found it difficult to select problems that the students would have a sufficient physics background to solve and find meaning in and the reaction from the students was very mixed. Apart from the physics background necessary for the problems and examples, students found it annoying to buy a book that contained much more material than what was covered in the course. Several chapters in the beginning of Arfken discuss topics with which the students were already familiar from dedicated courses in mathematics and many chapters towards the end included material that was not relevant to the course.

Lecture notes

Without a really good alternative, I decided to return to the Swedish textbook and write a set of lecture notes on variational calculus to supplement it with the missing material. Hoping that the lecture notes might help a larger set of students than those I was teaching at the time, I decided to write in English rather than Swedish. This turned out to be the best fit for the course that I had tried so far.

At this point, I had already been using Physics Forums for some time. I had spent quite some time in the homework forums and people appeared to appreciate my written replies, which was also soon underlined by the homework helper and science advisor badges. Furthermore, I was on the lookout for a hobby project. Where some people learn how to play a musical instrument or develop an affinity for stamp collecting, I decided to dedicate my time to extending my lecture notes to cover more parts of the course and eventually the idea of writing a full text specialized to my student’s needs took shape.

Deciding on topics

The first thing that was necessary was to define an outline of exactly what I wanted to write. One possible option would have been to just cover the topics of the course itself, but there was also another material that I wanted to include. My department was also giving an introductory course on vector and tensor analysis earlier in the academic year and I was also teaching an elective follow-up course covering Lagrange’s and Hamilton’s formulations of classical mechanics. Furthermore, I was also giving a course in special relativity at the master level, where I found that one major hurdle was that students had forgotten (or never really learned) most of their tensor analysis. In order to create a text that would cover most of my student’s needs, I decided to include the following topics:

1. Vector analysis.
2. Tensor analysis.
3. Modeling physical systems using PDEs.
4. Function spaces.
5. Series and transform solutions.
6. Green’s functions.
7. Variational calculus.
8. Calculus on manifolds.
9. Classical mechanics.
10. Electrodynamics.
11. Special and general relativity.

I had intended the last three topics to introduce new physics subjects to the students, using the mathematics introduced earlier in the text. However, as time went by, I realized that the two latter topics would make the text very extensive and would essentially result in books of their own if I covered them to the extent that I wanted to. If you check out the table of contents for my book, you will find that the structure above is essentially the same, apart from the electrodynamics and relativity parts. A chapter on symmetry was later added as I found it to be a topic in which many students in the master program were lacking knowledge. It also provided me with an opportunity to discuss the use of symmetries in modeling and allowed the addition of some nice insights later in the text.

Once the scope of the text had been defined, I needed more structure and an idea of what would be included in each chapter. Before writing anything, I sat down with a notebook and dedicated one page each for writing down the topics I wanted to cover in every chapter and their ordering. I must admit that I at this time did not have a clear understanding of how long it would take to complete the text, but I did realize that it would be a massive undertaking.

Selecting the tools and starting to write

Being used to writing scientific articles and having some experience of larger projects from my Ph.D. thesis, I knew that there was really only one option for typesetting and organizing the text, LATEX. As it would later turn out, the publisher, fortunately, agreed with this particular choice. For the figures, I decided that the best course of action was to create everything from scratch in order to avoid possible permission issues further on. At this stage, I had not yet decided exactly what I would do with the final text and one option that was on my mind was to make the final PDF available online. I will discuss the final decision later on. Most of the figures in the book were created using Xfig, but there are some notable exceptions, where I took photos that were later edited in Gimp.

With the process of writing my Ph.D. thesis in (not so fresh) memory, I also decided to write every chapter in a separate LATEX-file and include them all using a master file. The first order of business was to set up this master file and a structure that I could work with. I chose to use a generic LATEX book template and created one file for each chapter, in which I introduced all of the structure I had earlier written down in my notebook. I now had a skeleton of a textbook with the title “Introductory Mathematical Methods for Physicists.” Although I would review the structure of each chapter before writing it and made some changes along the way as I realized that some additional material was needed or that things were better presented in a slightly different order, this skeleton was very reminiscent of how the book is structured today.

Once the structure was in place, I started writing from the beginning and slowly worked my way towards the end. I vividly remember starting to write the first chapter on a weekend when I had nothing else to do. Before long I also needed to start constructing different figures, which I initially did when necessary. Although Xfig is a great tool for making vector-based graphics, I soon realized that I also wanted something more. In particular, I needed a figure of a hand in order to demonstrate the right-hand rule in what became Figure 1.3. Being a lousy sketcher, I decided to base the figure on a photograph instead. Applying several Gimp contour filters, importing the result into and adding the arrows in Xfig gave the final result. Of course, before taking the photo, I needed to find an appropriate hand to act as a model. Luckily, I have two of my own and the hands you will find in the book are mine. I say “is” since I needed the other hand to hold the camera. The final figure also has a mirror image of the original image in order to also demonstrate a left-handed set of vectors. I will leave it up to the reader to figure out whether the hand depicted in the figure is actually my left or right one.

Later I decided that it was more efficient to leave the figures empty with a comment describing what I wanted to show and construct all the figures of each chapter at the same time.

Once I had written about 20 pages in the format I was using, which contained slightly less text per page than the format you will find in the printed book, I decided to print what I had so far to get a feeling for how it might look in the end. I was rather happy with the resulting look and found some encouragement in that. Had this not been the case I am not sure that the book would ever have been completed. With this, the long process of writing had begun.

The long process

The actual process of writing a book of the size in question is a rather outdrawn one where not much of particular interest occurs. Rather than going through it chapter by chapter, I will just summarise how I approached the task.

As already mentioned, the book was my hobby project. On several occasions, my wife has told me she was astounded by the fact that I could write at the same time as I was watching TV, but whether that is a result of efficient multi-tasking or a testament to the average information conveyed by your average movie or TV-series I will leave unsaid. Apart from evenings and weekends, my daily commute was of the order of one hour one-way. Being otherwise wasted time (posting on Physics Forum using my phone aside), I started filling it with tasks related to my text. At first, the tasks I would do during the commute were mainly to bring out a notebook to go through the maths behind the next section, in particular when longer arguments were needed and I wanted to get the idea right before putting it in print. However, as time went on, this evolved into also taking out my laptop and writing entire sections. In the end, a non-negligible part of the book was actually written in a subway car.

For the figures, I would generally complete the text of a chapter before constructing its figures. Once it was time to do so, I would go through the entire chapter and make small rudimentary sketches of what I wanted to show in a notebook. Often this would result in several pages of tiny pictures, which were then realized in Xfig or by other means. With the order of 30 figures in a chapter, this would generally keep me occupied for an entire weekend per chapter.

My drafts for the figures of Chapter 10. They look much better in the final version, I promise.

The long process naturally also involved proofreading the text. While being a tedious task, it did give me something different to do and provided some variation, although I must admit I was lagging behind by a few chapters towards the end.

Completing the text

After roughly one and a half years of spending a large portion of my free time writing about physics (do not feel bad for me, I enjoyed it immensely), I was approaching the end. The page count was rapidly approaching 900 and I had decided to leave electromagnetism and relativity out of the text for several reasons. Apart from making the text immense and likely too broad in scope, I felt that it would be sufficient to include the classical mechanics chapter as an illustration of how the methods in the book can be applied to new settings. I would also be lying if I said that there was not a large part of me who also wanted a completed project at that time. Once all the text was in place and I had been through an entire round of proofreading, the time to decide what to do with the text was approaching fast.

A tough decision

The decision on what to do with the text was not an easy one. When I took the decision to write in English rather than Swedish, my idea had been to try to reach as many interested students as possible, but how would I accomplish this? There were three options that crossed my mind:

• I could put the final PDF on my homepage and advertise it sporadically by linking to it when called for in Physics Forums threads.
• I could try to self-publish in the same style as former Physics Forums member Benjamin Crowell has done with his set of books.
• I could contact a publisher to try to get it published as a textbook.

All of these options came with different pros and cons. If I had put the final PDF on my homepage, it would have been freely available for anyone, but how would they find it and read it? After all, it was a 900-page document and you can hardly expect anyone to print all of that and most people will not want to read that on their screens. In fact, already when on the lecture note stage, which only covered parts of the final document, students asked me for a printed version. Add to that the complication of people finding it and relying on awareness of the text’s existence being spread mouth-to-ear. I did consider self-publishing for some time, but in the end, I decided that the best method to spread the text was probably still to rely on a professional publisher with an economic incentive for promoting it and having a good quality print.

Enter CRC Press

A few years prior, I had been in contact with an acquiring editor at CRC Press asking me if I had any ideas for textbooks and encouraging me to submit a textbook proposal. Therefore, after making the decision to try to get the text published as a book, I decided to explore this path further and sent an e-mail to the editor asking whether they would be interested in the text or not. The e-mail immediately bounced back with an automated reply that the editor was on parental leave. A few days later I got a reply from the editorial assistant telling me the editor would return in a few weeks and that they would be happy to discuss the issue once she was settled in again.

At the end of September 2016, the editor replied and after some short discussions, I was encouraged to submit a textbook proposal. Such a proposal involves providing quite an extensive amount of information about the textbook, such as the number of pages, the number of figures, and the number of equations as well as making summaries of the target audience, the typical expected price, what classes would make use of the textbook, etc. Furthermore, a survey of the possible competing texts already available on the market should be provided.

Although I essentially had a completed manuscript at that time, it was my understanding that it is generally more common to make the proposal before the bulk of the text is actually written. However, having written most of the text already, many of the quantitative questions were rather easy to answer. Additionally, the proposal should include summaries of the intended contents of each chapter and if possible any samples of text that could aid in the evaluation. Since I already had the text, I provided two of the chapters (Chapters 3 and 9) as sample material. After submitting the proposal at the end of October, a period of about five weeks when I did not spend much time with the manuscript and mainly waited for the response started.

A mountain of reviews

In the afternoon of December 6, 2016, an email from the editor appeared in my inbox with the subject “proposal reviews received!” Like most people, I am not a big fan of being evaluated, but the exclamation mark in the subject already took some of the nervousness away. Opening the email, it turned out to be quite long with seven(!) reviews attached and an extensive analysis of what they said. Being used to having one reviewer when publishing scientific papers, having seven took me a bit by surprise, but after thinking some time about it, it does make perfect economic sense from the publisher’s side. While the revenue from publishing scientific journals is based on subscriptions and not the overall quality of a single paper, a publisher needs to ensure that there is high quality and reasonable demand for a textbook before spending resources on the publishing procedure.

Overall, all of the reviews were quite positive and provided a large amount of useful feedback, both for the publisher and for myself in terms of included material. Just like the textbook proposal involved answering a large number of questions from the publisher, so apparently did making a proposal review. The questions put to the reviewers included everything from the quality of the material itself to questions about the market, the most direct of them being “Do you recommend that we publish this book?” to which none of the reviewers had answered “no” and most were quite emphatically positive too. However, my personal favorite reply to the question was the honest “I am a physicist, not a book publisher.”

Apart from being generally positive, there was one thing that all of the reviewers agreed on. The word “introductory” should be removed from the title and the target audience of the book should be graduate or advanced undergraduate students. Since I did not have any particular problems with this, I was more than happy to adjust to this assessment.

I spent the next few evenings going through the reviews in detail and considering what they had to say about the text in particular. After discussing my thoughts on the reviews with the editor, she decided to go ahead and propose to the editorial director that the book should be published and that I should be made a contract offer.

Signing a contract

I received the first contract proposal a week or so before Christmas. At this stage, several things had to be settled, since the contract is what binds you to the publisher and vice versa. Many details about the final manuscript, such as the intended number of pages, were laid out in the contract. After discussions regarding several of the paragraphs, including the deadline, how the rights for the manuscript would be handled, how possible future editions would be written, and royalties, we ended up with a contract that was acceptable for both parties. Regarding the deadline, it was initially suggested that it should be put in mid-2017 since the manuscript was essentially completed already. However, in order to make sure to be able to deliver, I pushed to have it at the end of 2017 as I felt that there were still several things that needed to be done based on how the manuscript needed to be updated and proofread before submission. Finally, the contract was signed electronically by myself on Christmas eve and by the editorial director five days later. As fate would have it, I think I am about to receive my author copies almost exactly one year later.

Working to complete the manuscript

Already before signing the contract, I was aware that a solutions manual would probably be required. It had also been a request from several of the reviewers (although some did not like the prospect of students possibly getting access to solutions – there are always several different opinions on this among teachers) and so in parallel to the process of signing the contract, I started writing up solutions to all of the problems. In particular, I spent a lot of time doing this over the Christmas holidays, completing the order of 250 solutions over the course of two weeks. We all have our hobbies.

Although the solutions manual had a later deadline than the manuscript itself, I did discover some issues with the problem statements while writing the solutions and so I made it a priority to work through all the problems to make sure that they were solvable with the given information and at a more or less appropriate difficulty level.

In connection to the contract discussions, I also got access to the LATEX template to be used for the book. Although it decreased the page count from a mighty 900 to around 650, I immediately took a liking to the visual impact. It was probably at this point that I finally let myself change the reference to the text in my head from “lecture notes” to “book”.

After completing the solutions, I identified a number of issues that had to be dealt with and ordered them in terms of what would be the natural workflow, expecting each step to take between one and two months based on how much time I would have during evenings and weekends:

• Converting all figures to grayscale. While just keeping the manuscript as lecture notes, I had initially constructed all figures using colors. However, to save printing costs and thereby making the book more competitive, it was necessary to convert all the figures to grayscale. At this point I also took some extra time to improve upon several of the figures, essentially ending up with the final versions that you will find in the book.

• Adding new material.

  Based on the comments of the reviewers, several new passages had to be written and incorporated into the text while maintaining a natural flow. At the same time, the new material could not be too extensive in order to respect the set page limit.

  

  Beginner steps in the art of bookbinding. Here showing the proofreading copy of the solutions manual on top of the proofreading copy of the book itself.

• Proofreading

  . I wanted to go through all of the text at least one more time and make the changes I found necessary. One problem I did run into at this point was to find a reasonable way to carry the text around. In particular, I wanted to be able to carry all the text with me on public transport as I would largely spend my commute reading. Carrying 700 pages that are not bound together around was clearly unfeasible and to be able to do this I decided to take up the art of bookbinding. After reading about some different techniques on the internet, I made an attempt and was actually pretty satisfied with the result (see figure). However, I am very sure that CRC Press will be better at checking that

  all

  pages are in the correct order and with the correct orientation than I was – a major part of chapter 9 turned out backward. Still, there was something special about holding what essentially amounted to a book that I had both written and bound myself.

  

  Not a professional bookbinder after all …

Time to submit

At long last, after revising many details of the book again and going through all of the figures to check for consistency in style and presentation, the time had come to let go of the manuscript. It is not an easy thing to do when you have worked on a project for such a long time to tell yourself that it is completed and I can assure you that this case was no different. Although I knew that I would have opportunities to make minor revisions at steps along the way, there is always the feeling of insecurity mixed with the dread of losing control. I probably hovered over the submit button in the CRC Press file uploading system for several minutes and then had my wife do it for me. She seemed to have no problem whatsoever in sending away something that had been competing for my free time.

In the end, I did submit the completed manuscript only a few weeks after the originally proposed deadline and probably could have forced myself to complete it sooner. However, it never hurts to have some extra time in order to avoid a feeling of stress in the last moments of preparation.

The production process

The manuscript was now off my hands and to be fair, I cannot tell you much about the production process other than the fact that I have not been very involved in it. The major things I have had to do since submission has been to accept the title proposed by the publisher (actually, they do not really need me to accept it, it is one of the few things you really do not control as an author – the contract only requires the publisher to consult with the author), giving my input and thoughts on the cover art, and make some alterations to the manuscript based on the result of the publisher’s proofreading. In the end, the cover art is a photograph of a catenary somewhere in Stockholm with a stream running behind it – along with my own scribbles of some mathematics that can be used to describe them. Luckily, my own proofreading seemed to have been relatively thorough as there were actually not many things to take care of apart from some minor comments every three or four pages on average and some restructuring of the book’s front matter.

Here we are today

So finally, the time has come. The book is now in print and most likely available in an online bookstore near you. Just for reading to the end of this Insight, CRC Press has been kind enough to provide the readers of Physics Forums with a discounted promotional price if you want to buy the book:

S**ave 20% off the purchase of ‘Mathematical Methods for Physics and Engineering’ when you order online at https://www.crcpress.com/9781138056886 and enter Promo Code MPE18*.* Free standard shipping when you order online.

Orodruin

Associate professor in theoretical astroparticle physics. He did his thesis on phenomenological neutrino physics and is currently also working with different aspects of dark matter as well as physics beyond the Standard Model. Author of “Mathematical Methods for Physics and Engineering” (see Insight “The Birth of a Textbook”). A member at Physics Forums since 2014.

---

Write Tools

Here are some suggestions of tools you can use to make your drawings:

• GeoGebra: Interactive geometry, algebra, statistics and calculus application, intended for learning and teaching mathematics and science from primary school to university level[ Wikipedia].
• Inkscape: Can be used to create or edit vector graphics such as illustrations, diagrams, line arts, charts, logos and complex paintings [Wikipedia].
• Corel Draw: Vector graphics editor, like Inkscape, but more professional and not free.
• Tikz: Tool to create graphic elements in LaTeX, but you have to code. (Examples)

I believe you should try GeoGebra first. It might be entirely suitable for you, and I think it’s the easiest to work with.

Looking up video tutorials about these tools might help a lot.

To import the figures to your Latex document, make sure you always save your drawings in a vector format (such as SVG, EPS or PDF); this format will give you the best quality. Also remember to make a copy of each drawing in an editable format (so if you want you can edit it afterwards with whichever tool you used to create it).

---

作者：Linkzero Tsang
链接：https://www.zhihu.com/question/23116631/answer/117320791
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

\1. 那时应该还没有TeX/LaTex等专业排版系统，那么那些复杂的数学公式和函数图像等，又是如何排制出来的呢？（顺带问一下该书字体为何，似乎同现在的宋体有些不一样）

公式用专门的铅字排。图像是手工制图后，制成凸版，再印刷。下面这张图是在排版中，将铅空 * 所占位置填黑的示意图。可以看到公式中的各个铅字是怎么排的：

• • * 铅空是金属活字时代，排版时用以填充位置、固定铅字的各种大小的铅块。

来源：http://ultrasparky.org/school/pdf/Rhatigan_Monotype_4-line_math.pdf

而宋体是一类字体，书上用的宋体和今天常用的 Windows 内置的「宋体」（由中易设计及制作）不一样是再正常不过的事情。这套字体的具体名称和背景信息为何，在今天恐怕已不可考。不过到此书当年的出版社和印刷厂，或许能够找到一些蛛丝马迹。

\2. 国内现代数学书籍是采用TeX/LaTeX等套件排印的么？

有用 TeX / LaTeX 排的，也有用其他排版软件——比如方正书版之类——来排的。参见：商业出版公司真的有用 LaTeX 的吗？ - 排版

---

商业出版公司真的有用 LaTeX 的吗？

latex排版的书刊有什么明显的特征吗？

准确点说，印刷品基本上只有商业出版公司才能做，国内则是强制要求（否则算非法出版物）。LaTeX 排版的印刷品当然也不例外。TeX/LaTeX 的应用主要在学术出版领域，特别是数学、物理、计算机、化学等计算机相关学科，以及心理学、语言学等，使用它的出版物还是很多的。

TeX 本身是为了出版计算机科学著作 TAOCP 而编写的软件，而 TAOCP 是由 Addison Wesley 公司出版的。TeX 是 AMS（美国数学会）的商标，被与其相关的几乎所有期刊、书籍使用。AMS 本身也是出版商，一直在 TeX、LaTeX 上投入金钱和精力。从早期的 AMS-TeX、AMS Fonts，到 1990 年发布 AMS-LaTeX，到 LaTeX2e 发布后的 amsmath、amsfonts 宏包，都是由其主导开发的。与 AMS 类似，APS、ACM、IEEE、ACS、APA 等美国学术机构都大量使用 LaTeX。Springer 出版社，Elsevier 出版集团等出版商，在出版学术文集、教材、专著时，也都大量使用 LaTeX。这样的例子很多，如 Reinhard Diestel: Graph Theory, 3ed, Springer：

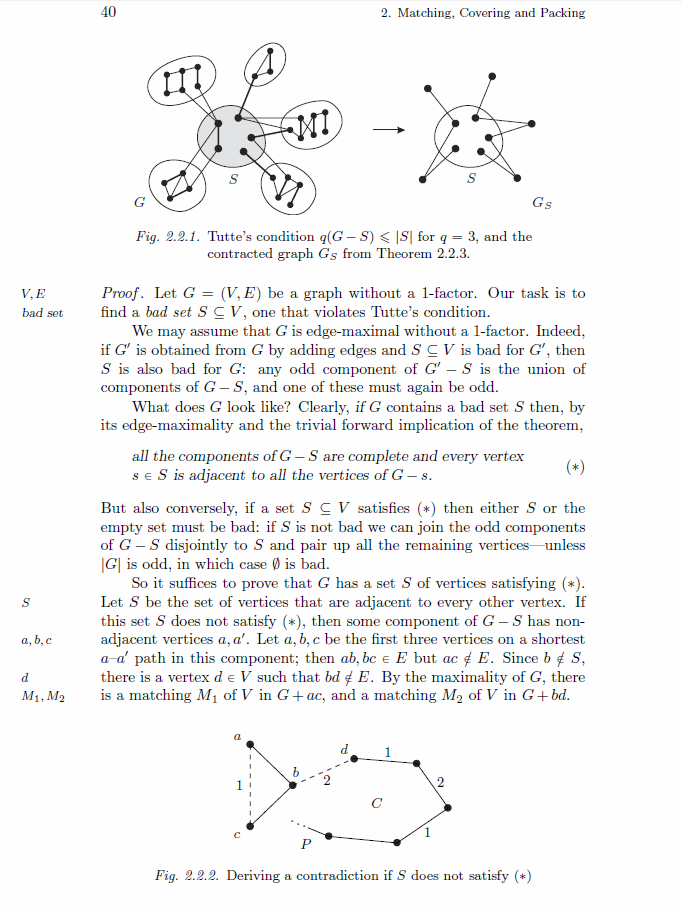
又如 CLRS, Introduction to Algorithms, 3ed, The MIT Press：

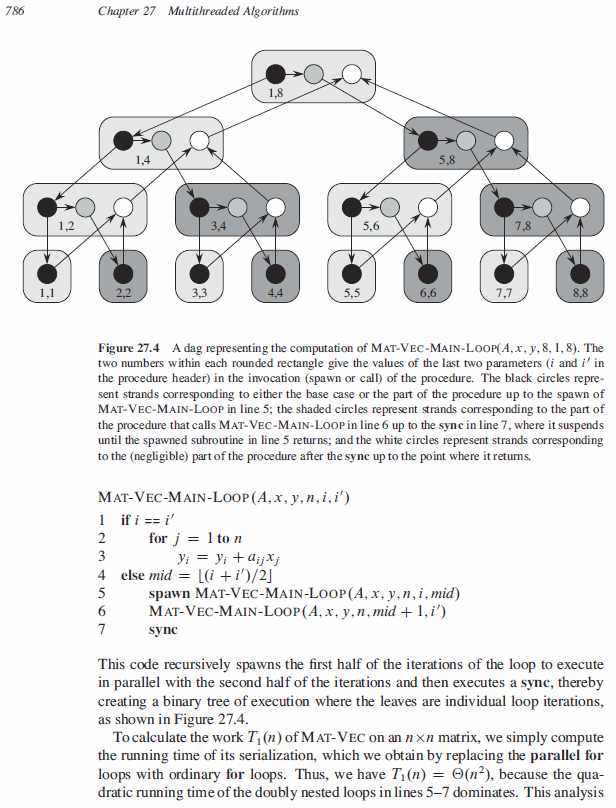
再如 David R. Hanson, C Interfaces and Implementations: Techniques for Creating Reusable Software, Addison Wesley：

国内科学出版社，高等教育出版社，机械工业出版社，清华大学出版社，北京大学出版社等等，我们也都能见到使用 LaTeX 排版的教材和专著。如冯荣权，宋春伟《组合数学》北京大学出版社：

又如 Alexander Stepanov《编程原本》，机械工业出版社：

TeX 本身的成功就在于高质量的数学排版和一套成功的数学公式记法。因此 TeX/LaTeX 主要在数学公式较多的科技排版中使用。但这并非绝对，比如盖鹤麟提过 Duke 大学出版社的一部分人文社科类书籍和期刊也使用 LaTeX 排版。下面另举一个在 TeX.sx 上看到的例子，Carlo Collodi 的文学作品《Eachtra Phinocchio》，出版商 Coiste Litriochta Mhuscrai：

LaTeX 的一个重要特点，是主要由作者本人编写代码进行排版，而非出版商。对作者来说这是一大优势，即作者对自己作品的最终呈现方式有了极大的掌控权，从而可以最大限度地避免排版过程造成的表意错误。（我记得大约是 AMS 的 Barbara Beeton 曾说 AMS 内部有一条编辑准则就是没有绝对把握就不要改作者的代码，因为很可能改变意义而被作者喷回来。出处不明。）反过来，这也成为一种劣势，就是 LaTeX 比纸笔或 MS Word 等字处理工具有较高的学习成本，作者需要花费更多的精力使用这一工具（注意这只是对作者的，对出版方 TeX 并不比其他排版工具更难使用）。这也是为什么使用比较少的原因。

---

https://en.wikibooks.org/wiki/LaTeX

https://www.latex-project.org/

http://www.ams.org/publications/what-is-tex

http://www-math.mit.edu/~dav/writing.html

https://en.wikibooks.org/wiki/LaTeX/PGF/TikZ

GSM

https://web.cs.ucdavis.edu/~amenta/w10/writingman.pdf

https://faculty.math.illinois.edu/~reznick/good-math-writing.pdf

https://www.ams.org/journals/notices/202106/rnoti-p930.pdf

---

Math Major Roadmaps

This document outlines “roadmaps” of course options for undergraduates interested in particular fields and applications of mathematics. Each roadmap consists of three stages:

• Stage 1: Introductory courses with few prerequisites, accessible to a typical sophomore.
• Stage 2: More advanced classes for students who have mastered several stage-1 classes.
• Stage 3: The most advanced classes, often beginning graduate-level subjects, for students who have mastered many stage-1 and stage-2 classes. (Many math majors will never take a stage-3 course, and that’s okay!)

The stages also reflect priorities—for example, students interested in pursuing analysis probably want to take 18.100 as early as possible, whereas a student pursuing mathematical finance might take it later to deepen their understanding.

In each specialized field or application of mathematics below, we list courses that could be relevant for a career in that field—not just courses narrowly in that specialization, but also useful courses in broadly related areas. On the other hand, these specific courses are not requirements to pursue that field.

Note that a math degree requires 18.03 and 18.06/18.700/701 (or approved substitutions thereof), but these are not necessarily listed in every roadmap below, nor do we list GIRs like 18.02.

Pure Mathematics

General comments: Below is a list of research areas. As an undergraduate, however, you should not conceive of yourself as specializing in one or another of these areas. A much better idea is to gain experience in several of them. You may find yourself taking more courses in one or another area, but all of these fields of study reinforce each other.

Stage 2, but not specific to any particular area: 18.821 (Project Lab in Mathematics) is a great introduction to some essential skills (research, teamwork, and communication).

Algebra

• Stage 1: 18.700+18.703, 18.700+18.701+18.702 or 18.701+18.702
• Stage 2: 18.704, 18.715, 18.721, 18.782
• Stage 3: 18.705, 18.706, 18.725, 18.745, 18.755, 18.783

Analysis & Geometry

• Stage 1: 18.100, 18.700/18.701
• Stage 2: 18.101, 18.102, 18.103, 18.104, 18.112, 18.152, 18.950, 18.994
• Stage 3: 18.125, 18.155, 18.156, 18.952, 18.965, 18.966

Logic

• Stage 1: 18.510, 18.701 or 18.700+18.703
• Stage 2: 18.400, 18.404, 18.504
• Stage 3: 18.515 (not offered regularly)

The MIT Philosophy department also offers subjects in logic: 24.241–24.245 and 24.711. Also consider logic classes at Harvard.

Number Theory

• Stage 1: 18.700+18.703 or 18.701+18.702, 18.781
• Stage 2: 18.704, 18.721, 18.782, 18.784
• Stage 3: 18.705, 18.725, 18.783, 18.785

Probability & Statistics

• Stage 1: 18.065, 18.100, 18.600, 18.700/18.701
• Stage 2: 18.102, 18.103, 18.112, 18.200, 18.211, 18.615, 18.642, 18.650
• Stage 3: 18.125, 18.675, 18.676, 18.677, 18.338, 18.416, 18.424, 18.655, 18.657

Topology & Geometry

• Stage 1: 18.100, 18.112, 18.701+18.702 or 18.700+18.703, 18.900, 18.950
• Stage 2: 18.101, 18.102, 18.901, 18.904, 18.952, 18.994
• Stage 3: 18.116, 18.155, 18.721, 18.755, 18.782, 18.905, 18.906, 18.965, 18.966

Applied Mathematics

Stage 2, but not specific to any particular area: 18.821 (Project Lab in Mathematics) is a great introduction to some essential skills (research, teamwork, and communication).

Combinatorics

• Stage 1: 18.100, 18.200, 18.400, 18.600, 18.701+18.702 or 18.700+18.703, 18.900
• Stage 2: 18.204, 18.211, 18.212, 18.112, 18.404, 18.410, 18.453, 18.721, 18.781, 18.901, 18.950
• Stage 3: 18.217, 18.218, 18.225, 18.226, 18.338, 18.455, 18.615, 18.705, 18.715, 18.725, 18.745

Computer Science

• Stage 1: 18.06/18.700, 18.062, 18.200, 18.330, 18.600, 18.650, 18.701
• Stage 2: 18.204, 18.211, 18.400, 18.404, 18.410, 18.424, 18.434, 18.453
• Stage 3: 18.337, 18.415, 18.416, 18.425, 18.435, 18.437, 18.455, 18.783

Students in this area should strongly consider supplementing their math courses with several courses in computer science; see the 18c major requirements for typical choices.

Economics and Finance

• Stage 1: 18.03, 18.05, 18.06/18.700, 18.065, 18.300, 18.330, 18.600, 18.650
• Stage 2: 18.100, 18.152, 18.303, 18.453, 18.642
• Stage 3: 18.103, 18.125, 18.675, 18.676, 18.677, 18.335, 18.337, 18.338, 18.352, 18.353, 18.355, 18.615, 18.655

Students interested in economics and finance should strongly consider supplementing their math courses with several classes in course 14 and 15, if not a minor or double major.

Computational Science and Engineering

• Stage 1: 18.03, 18.06/18.700, 18.04, 18.05, 18.062, 18.065, 18.200, 18.303, 18.330, 18.600, 18.650, 18.S190, 18.S191
• Stage 2: 18.100, 18.404, 18.434, 18.410, 18.701
• Stage 3: 18.335, 18.336, 18.337, 18.338, 18.367, 18.415, 18.437

Students in this area should consider supplementing their math courses with several courses in computer science, both for software engineering (e.g. 6.0001, 6.009) and numerical methods or optimization (e.g. 6.215, 6.339). For students interested in computational modeling of physical systems, see also the Physical Applied Math classes below.

Physical Applied Math

• Stage 1: 18.03, 18.04, 18.06/18.700, 18.300, 18.303, 18.330, 18.352, 18.353, 18.354, 18.600, 18.650
• Stage 2: 18.100, 18.112, 18.152, 18.384, 18.417
• Stage 3: 18.102, 18.103, 18.305, 18.306, 18.335, 18.355, 18.357, 18.367, 18.369, 18.376, 18.377

Students interested in physical applied mathematics should strongly consider supplementing their math courses with at least 2–3 non-GIR courses in physics and/or engineering, depending on their field of interest, if not a minor or double major.

Statistics and Data Science

• Stage 1: 18.05, 18.06/18.700, 18.062, 18.065, 18.100, 18.200, 18.330, 18.600, 18.650, 18.701
• Stage 2: 18.102, 18.112, 18.204, 18.642
• Stage 3: 18.125, 18.675, 18.676, 18.335, 18.338, 18.615, 18.657

Students in this area should consider supplementing their math courses with courses in computer science on machine learning and courses in economics on econometrics.

https://math.mit.edu/academics/undergrad/roadmaps.php

http://catalog.mit.edu/archive/

---

书单推荐(1)：复变函数/复分析的入门教材

近期准备重学一下复分析，大三上的复变函数约等于没学(太菜了)…最近准备重拾一下，主要是为之后自学黎曼几何、黎曼曲面做准备。网上搜了好几天的资料，打算把书单列述在此，供其他数学爱好者参考。由于本人水平实在有限，本书单只强调入门，所以诸如Rudin的Real and Complex Analysis这类的书我就不推荐了…认为Rudin这套书足够基础的知友们可以忽略本文。

以下为8本比较不错的复分析/复变函数教材，我标注了最新版本，以及中英文版本的情况。排名不分先后：

（1）Brown的Complex Variables and Applications(7th edition)

（经提醒，最新版已经有第9版）机械工业出版社有翻译版，书名是复变函数及应用。美国密歇根大学的教材，非常基础，例子也比较多，适合自学。这本书尤其注重复变函数在物理、流体流动、热传导以及偏微分方程的边值问题中的应用，对工科同学来说应该也是比较友好的。

（2）拉夫连季耶夫, 沙巴特的复变函数论方法(第6版)

高等教育出版社翻译。老毛子的经典教材，也很基础，适合自学。这本书的特点是包含大量几何观点，易于理解。

（3）Ahlfors的Complex Analysis(3rd edition)

机械工业出版社有翻译版，也有授权的影印版。分析大师Ahlfors的经典之作，非常好的教材，比较适合入门，也包含大量的几何观点。在知乎上看到有知友表示第2版更好，我还没有读过，所以不太清楚，之后有空更新。

（4）Tristan Needham的Visual Complex Analysis

图灵社区&人民邮电出版社在年初推出了2021全新再版，书名是复分析：可视化方法。这本书非常有意思，它不像是一本教材，反而更像一本复分析中的数学思想巨著，全书另辟蹊径，从几何的角度来阐述作者的理解。或许它不是一本严谨扎实的复分析教材，但如果你有一定的基础，该书的几何思维或许能给你更深的理解。值得一提的是，这本书的译者是武大齐民友教授，他在翻译中对原书做了锦上添花的一些注解，可以说是少有的比原版更好的翻译版。

（5）龚昇的简明复分析

北京大学出版社/中国科学技术大学出版社出版。书的厚度确实是相当“简明”了，书中也嵌入了不少几何观点，将微分几何与Picard大定理联系起来非常有特色。北大的第一版比较老，据说书里的小错误比较多，但是中国科大出版社在09/10年重新出了第2版，不知道该版本如何。（更新：emmmm似乎第2版的错误也不少…）

（6）史济怀, 刘太顺的复变函数

中国科学技术大学出版社出版。可能是目前国内作者写的最好的复分析教材之一，逻辑很清晰；不过书的内容不是很多，比如Picard定理就没有给出证明。该书是龚昇简明复分析第一版的升级纠错版（虽然部分习题似乎也有些小问题），值得一读，可惜貌似已经绝版，某宝也很难买到了。

（7）Stein的Complex Analysis

机械工业出版社有翻译版，世界图书出版公司有授权的影印版。又是一篇著作，调和分析Stein分析四部曲之一。相比Ahlfors的复分析，Stein的版本分析味更浓厚，非常严谨。我不确定该书是否有前几本那么“浅显”，但如果有志于从事分析学的话，由此书入门一定是非常好的。另外，Stein的习题质量非常不错。

（8）Conway的Functions of One Complex Variable

世界图书出版公司有授权的影印版，无翻译版。该书有2卷，GTM011与GTM159，肯定是好教材，虽然我并不确定该书是否适合入门（反正我看到GTM就暂时先放弃了…）

---

另外，钟玉泉的复变函数与余家荣的复变函数是国内很多学校使用的教材，但是内容似乎不是太全，我也没仔细了解过，这里就不列述了。

我在开头已经说明，我希望重学复分析主要是基于“为之后自学黎曼几何、黎曼曲面做准备”，因此，我个人选择Ahlfors的Complex Analysis作为主要教材，齐民友翻译的Visual Complex Analysis作为重要参考，龚昇、史济怀、拉夫连季耶夫的作为辅助参考。

***以上英文书籍，除齐民友翻译的那本外，其他均强烈推荐阅读英文原版！***（只要你的英语阅读能力不是特差都可以）本人询问+实测，哪怕是授权影印版，清晰度都还是非常不错的。

*这8套书的电子书以及对应的翻译版本我已在课余时间收藏过，以下为链接：*

链接：https://pan.baidu.com/s/1FxAJhZdKthT4sj8P0U27Ow

提取码：q5fs

书单推荐(2)：线性代数/高等代数的入门&进阶教材与相关资源

这一篇推荐几本线性代数/高等代数的入门&进阶教材。相比微积分/高等数学/数学分析，线性代数/高等代数这门课程的性质决定了要讲好它、学透它可能更不容易，无论是上课教学还是书本，不同的选择在学习效果上会有很大的差异。这几周有许多数学系与非数学系的低年级同学咨询过我这方面的书籍推荐，故决定总结于此。

首先需要说明的是，根据国内数学专业的教学体系，“高等代数”这一说法其实是不太准确的：一方面处理的基本都是线性问题，另一方面大部分授课内容中也并没有体现“高等”一说。所以，同样的内容，***称之为“线性代数”其实更为合理***，非数学系的同学所学的线性代数可能也只是相似内容的简化版。因此，对于数学系的同学，也无须认为以下出现的“Linear Algebra”不够高端，其实细细品味还是有非常多深刻的观点蕴含其中的。

以下是书籍推荐，根据不同层次与类别，我将它们划分为四类，并标注了最新版本，以及中英文版本的情况。

（一）入门教材

首先是2本非常不错的的入门教材，***这几本书籍至少对于非数学系的同学都是非常友好的（也确实更适合非数学系），完全可以阅读。***排名不分先后：

（1.1）Gilbert Strang的Introduction to Linear Algebra(5th edition)

无翻译版，清华大学出版社有授权的影印版。这本书在知乎上也已经是非常受推荐了，MIT的教材，今年清华大学也引入该书作为工科的线性代数教材。该书难度比较小，易于理解，可以认为是入门线性代数最好的一套书籍之一。该书相关的资源也非常多，b站上有Strang老爷子亲自授课的视频（中英文对照），互联网上也有对应的课程主页、习题答案以及他人的学习笔记可供参考。我在这里列出对应的链接：课程主页*，*双语教学视频*，*参考答案*，*学习笔记。

（1.2）David C. Lay的Linear Algebra and Its Applications(5th edition)

机械工业出版社有翻译版。注意认清书名and以及作者David C. Lay，因为同名/相似名的书比较多。这本书的名气可能不如Strang那么响，但我个人认为质量完全不输于它。这本书的特点是包含大量的几何理解；采用比较现代的矩阵观点（证明与给出定义时采用*矩阵的列*而非矩阵元素，更能够简化一些论据并更好地体现向量空间的本质）；并附带非常多的应用实例（如计算机图形学、图像处理、动力系统、一些经济模型与工程模型）。书中许多知识点还夹杂着不少对应的*数值计算**的注解内容，这尤其对以后希望从事计算机科学、统计学、计算数学、工程学***方向工作的同学是非常有帮助的。另外，书里有大量不同类型的题目，难度不大但都很有意思。这本书对应的资料也是非常多的，这里就不列举了，我最近在读这本书，觉得非常有意思。

（二）入门&进阶教材

接下来是4本入门&进阶教材，这几本书籍比上面两本可能要略难、深一些，但是***对于数学系以及一部分数学思维还不错的同学来说仍然可以作为入门教材，后面三本都有配套的习题集性质的书籍，适合准备研究生考试的同学刷题强化***。排名不分先后：

（2.1）Sheldon Axler的Linear Algebra Done Right(3th edition)

人民邮电出版社有翻译版。大名鼎鼎的教材，该书在内容编排与叙述上完与国内传统书籍完全不同，抛开行列式而完全以线性空间、线性算子来切入，具有浓厚的数学气息，尤其适合以后希望从事数学研究的同学入门阅读（当然，包括但不限于）。即便国内许多数学系的同学在学完高代后，可能概念仍然也只是停留在矩阵、行列式的计算规则上，对线性空间与线性映射完全没有深入理解，因此该书作为加深理解的教材来说也是非常有用的，强烈推荐。互联网上也有该书的教学视频（英文）与习题答案，我在这里列出对应的链接：英文教学视频*，*参考答案1*，*参考答案2。

（2.2）丘维声的高等代数，以及高等代数学习指导书

清华大学出版社出版。两套书上下册加起来一共有4册，都是大部头，应该是中文教材里非常好的系列了。前面两册是教材，内容非常丰富，也有一定的深度、难度，还涉及了一小点抽象代数的内容，写得也很好；后面两册偏重解题技巧的指导，准备考研保研的同学可以用它来刷题，这4本书的习题质量都非常高。丘维声教授对这套书的授课视频也在b站上有，讲得非常好，可以配套学习，我把链接放在这里：教学视频1*，*教学视频2。

（2.3）蓝以中的高等代数简明教材(第2版)，以及高等代数学习指南

北京大学出版社出版。前面的教材分为上下2册，是北大经典的小黄书系列，我认为有一定深度、难度（个人觉得比丘维声版更难一些，对有些人来说可能不适合入门），但是这套书我没有细致看过，没有更多的了解。后面的学习指南属于内容思想的归纳+一部分习题，也是非常不错的，如果已经有足够的教材，仅希望做一些习题准备考试的同学，仅买这本也可以。

（2.4）姚慕生, 吴泉水, 谢启鸿的高等代数学(第3版)，以及高等代数(第3版)

复旦大学出版社出版。前面是教材，后面是对应的习题集。这两本书也是非常不错的，习题质量也很高，谢启鸿老师还专门有一个官方博客，上面有关于该书的习题答案、勘误等内容，学习之余可以作为参考，链接是：复旦谢启鸿 高等代数学习资源。

另外，李尚志的线性代数（中国科大教材）据说也是非常不错的教材，但我本人没有接触过，不好做评论。

（三）进阶教材

接下来是1本非常不错的进阶教材，这本书应该不太适合入门（大神忽略），最好是有一定基础后阅读：

（3.1）Peter Lax的Linear Algebra and Its Applications(2ed edition)

人民邮电出版社有翻译版。该书和David C. Lay同名，作者是数学大师Lax，观点较高，也有难度，绝对是好书，但由于本人水平较菜，还未读过，所以难以给出评价，基础比较好的知友们可以考虑。

（四）辅助阅读书籍

最后推荐1本非常不错的辅助阅读书籍：

（4.1）任广千的线性代数的几何意义

西安电子科技大学出版社出版。这本书的作者是工科人士，他从线性代数蕴含的几何观点的角度阐释了一些概念，在信息科学环境下应该说有一定的参考价值，可以作为辅助读物。当然，我个人觉得书中的一些内容有些牵强，本书也不能作为教材。

（五）几点重要说明

在末尾我有必要说明以下几点：

1. （2019.12.4更新）Strang和C.Lay的线性代数都是非常好的教材，但我认为它们*无论从难度还是内容侧重上都更适合非数学系或工科专业的同学*。如果你是*来自数学系尤其是希望从事基础数学研究**的同学，还是建议从第（二）部分开始入门，尤其是姚慕生版或丘维声版的高等代数***。
2. 如果你想真的对线性代数/高等代数有一定理解，**请务必放弃北大王萼芳版的高等代数！*（高等教育出版社，多数学校用的是第4版，现在已经出第5版了）我个人觉得这本书真的是一言难尽，然而我发现国内使用该教材的学校还非常不少，简直无力吐槽…如果本科数学系的你使用的也是这本教材，请务必在上述第（二）部分中挑选4本入门&进阶教材***中的至少1本来辅助学习！
3. 如果你们学校使用的是**自编教材*，请务必认真辨析***。有的教材可能是老师精心结合了各种优秀教材的长处并根据学生情况做的综合版本，而有些教材可能仅仅是完成“任务”…由于线性代数/高等代数的教材选择真的非常重要，因此，如果你认为是后者，也同样建议你选择其他教材辅助学习。
4. 线性代数/高等代数属于基础课程，上述教材不必都买，在适合自己情况的前提下有层次地选择即可。*尤其对于数学系的同学来说，除非是为了数学竞赛、保研考试或研究生初试准备，否则，在基础课程上花费太长时间（看过多同类教材或过多的刷题）是不值得的，继续后续课程的跟进学习更加重要。*
5. 接上方，如果针对保研参考与刷题的教材（因为事实上我也只了解保研，考研与竞赛并不一定适用），***姚慕生老师的书或者丘维声老师的书比较合适，其中后者比前者的内容更多、更广，当然大家根据自己的层次与时间精力选择自己合适的即可***。（注意这是教材，是否购买习题集是另一回事，习题集的选择也另当别论）
6. 以上涉及的英文教材，***强烈建议阅读英文原版！***（只要你的英语阅读能力不是特差都可以）

*前5套书的电子书以及对应的翻译版本我已在课余时间收藏过，更新下载链接如下：*

链接：https://pan.baidu.com/s/1U4q37PsnbTlqjKr3Kh8qHw

提取码：fg2y

书单推荐(3)：微积分/高等数学/数学分析的入门&进阶教材与相关资源

好久不见！这一篇推荐几本微积分/高等数学/数学分析的入门&进阶教材。在国内教学体系中，微积分、高等数学、工科数学分析等课程名一般由非数学系的其他理工科专业开设，数学分析课程则由数学系开设。

根据不同层次与类别，我将它们划分为三类，并标注了版本与语言等情况，对于部分书籍的相关资源（电子书、参考答案、教学视频等），我附上了链接，并在文末附上了多数书籍的pdf版本。

（一）微积分/高等数学的入门教材

（1.1）Thomas的Thomas’s Calculus(12th edition)

（英文已经有14th edition了）高等教育出版社有翻译版，书名是托马斯微积分。很经典的一套微积分入门教材，知识点讲得非常详尽、细致，例题与证明推导都很丰富，习题也不少（但大多比较简单）。但是缺点就是太过基本与详细，甚至有一些“啰嗦”，而且篇幅也非常大，阅读起来比较耗时，因此仅适合第一遍初学入门，或供工科同学查阅使用。

（1.2）A.Banner的The Calculus Lifesaver（普林斯顿微积分读本）

人民邮电出版社有翻译版，书名是普林斯顿微积分读本。同样是微积分的经典入门教材，相对托马斯微积分来说，这本的体量小了不少（当然和同济版相比依旧多了一倍），例题、证明、的量都减少了，且没有课后习题。需要特别注意的是，这本书的缺点是只包含一元微积分的内容，没有多元微积分（国外有一些微积分教材是会把一元微积分和多元微积分区分开来独立成书的），所以即使是对于国内工科高等数学的教学范围来说也有欠缺。

（1.3）James Stewart的Calculus(7th edition)

（英文已经有8th edition了）中国人民大学出版社有双语版，书名是微积分。这本书也非常经典，它的特色是书中包含了大量微积分知识点的实际应用，图文并茂，习题质量也很高。当然，这本书也是和托马斯微积分一样的大部头，足足1300多页…

（二）数学分析的入门教材

（2.1）陈纪修的数学分析（第3版）

我心中最好的两套数学分析的中文教材之一，分上下两册，另外还有配套的习题指南，也是上下两册。这本书讲得非常清楚，适当插入了一些应用实例和对应数值分析的内容，在知识点上比其他数分教材也更有广度一些，包含如极限相关的Stolz定理、无穷乘积、插值多项式、欧式空间的拓扑与泛函等内容。当然，这本书的习题质量也非常高。另外，b站上有陈老师2008年在复旦大学亲自讲授的数学分析教学视频，尽管录制时间和对应教材版本都比较老，但丝毫不影响学习的效果，我本人听过一部分，教学质量非常高，视频清晰度也不影响听课效果，强力推荐。视频链接贴在这里：

数学分析 复旦 陈纪修_哔哩哔哩 (゜-゜)つロ 干杯~-bilibiliwww.bilibili.com/video/av8042121?from=search&seid=3885775104197658640

（2.2）常庚哲, 史济怀的数学分析教程(第3版)

另一套我心中最好的数学分析中文教材就是它了，中国科学技术大学出版社出版，分上下两册。这本书是中国科大数学科学学院的教材，好评度和陈纪修老师那一套大致相当，质量很高，但是难度略有提升。课后的习题质量很高，也有一定难度（有些是竞赛题难度，比例题要难许多），习题分为练习题和问题两个板块，其中问题板块的题尤其难。这本书没有官方的课后习题解答，但据说很多题在徐森林的《数学分析精选习题全解》里都有答案。除此之外，知乎上有一份中国科大数院硕士

@顺数人

手写总结的习题解答，详见该专栏：

数学分析教程解析zhuanlan.zhihu.com/c_1213552747108392960

另外，史济怀老师也亲自用这套教材授过课，视频质量也非常高，把书中一些比较难的知识点基本讲透了。链接如下：

数学分析教程——史济怀_哔哩哔哩 (゜-゜)つロ 干杯~-bilibiliwww.bilibili.com/video/BV1X4411n7eb?p=1

（2.3）梅加强的数学分析

高等教育出版社出版，梅加强老师在其个人主页上也发布过LaTex的初稿版本（我已将pdf版本全部整理在文末）。这本书的特点在于篇幅只有区区600多页，用非常精简的篇幅描述了数学分析的最精华最核心的知识，叙述简洁而干净，可读性比较强。我本人没有仔细读过该书，但它也广泛受到推荐，。书中还简单涉及了n重积分、流形、度量空间、微分形式、Jordan测度等一些相对高观点的知识，这对于数学系同学进一步的学习探究有比较好的引领作用。这本书的习题据说和常庚哲史济怀的那一本有一些重复，也有很多题在徐森林的《数学分析精选习题全解》里有答案。梅加强老师也亲自使用这本教材在中国大学MOOC上授过课程，链接如下：

数学分析（一）：一元微积分_南京大学_中国大学MOOC(慕课)www.icourse163.org/course/NJU-1003628001?tid=1206775257

数学分析（二）：多元微积分_南京大学_中国大学MOOC(慕课)www.icourse163.org/course/NJU-1207130820

（三）数学分析的进阶教材

（3.1）Zorich的Mathematical Analysis(2nd edition)

高等教育出版社有翻译版，书名是数学分析。大名鼎鼎的俄式著作，这绝不是传统的数分教材，我对这本书看到过许多不同的评价，甚至两极分化，但讲解细致、内容完备是公认的优点，习题质量高且难也是公认的。当然，该书对于绝大多数数学系的同学来说都不适合入门，至少应先大致掌握一部分数分的核心思想才能阅读本书。很可惜，我几乎没能读过这套书，所以很难做出进一步的评价。

（3.2）菲赫金哥尔茨的微积分学教程（第8版）

高等教育出版社有翻译版，书名是微积分学教程。三册近2000页的大部头著作，内容详实，计算与证明的推导过程非常详细，而且包含了许多微积分的应用，堪称是当时古典微积分经典理论的巅峰。这本书的缺点在于篇幅过大，可能更适合用作字典查阅，另外内容基本没有涉及现代数学的一些观点，这对有志于从事基础数学的同学后续的学习来说，可能没有很好的衔接性。

（四）几点重要说明

1. 对于非数学系的同学，初学与入门可以使用第一部分推荐的三本教材（或其他同类教材），学有余力的情况下可以阅读第二部分或第三部分的书籍；
2. 对于数学系的同学（尤其本科之后仍打算攻读数学研究生，甚至未来希望从事数学研究工作的同学），建议直接跳过第一部分，着重选择第二部分的某一套书籍进行精读；
3. 国内高校大多使用的是华东师大的数学分析，但我认为它不如第二部分中的任意一套，这三套书即使作为参考也是很好的选择（当然，仅用一套学院指定的教材是远远不够的，你至少需要另外一套教材作为辅助参考）；
4. 其他诸如Rudin、陈天权、徐森林、陶哲轩、Stein等的数学分析教材我都不太了解，因此也不在此做任何评价。

*除陈纪修老师的那一套外，其他7套书的电子书以及对应的翻译版本我已在课余时间收藏过，以下为链接：*

链接：https://pan.baidu.com/s/143Omvue4UazyJQj1r6HSag

提取码：8kun

Thomas Calculus 最新到14th了哦。我刚刚在网上转了圈搞了份pdf回来。Thomas Calculus 14th Edition.zip

陈纪修老师的数学分析（第二版）

链接：https://pan.baidu.com/s/1fEWTnJ2n0qoI0wJYiYlV0w

提取码：kfa5

推荐两本：Peter Lax 的《微积分及其应用》《多元微积分及其应用》，科学出版社